| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- NLP
- animation retargeting
- Unreal Engine
- 모션매칭
- deep learning
- ue5.4
- multimodal
- ddpm
- 폰트생성
- WinAPI
- cv
- motion matching
- Few-shot generation
- Diffusion
- Stat110
- 디퓨전모델
- GAN
- 오블완
- Generative Model
- UE5
- dl
- CNN
- 언리얼엔진
- userwidget
- WBP
- 딥러닝
- RNN
- Font Generation
- 생성모델
- BERT
- Today
- Total
Deeper Learning
[UE5] MakeRotFrom 코드 분석을 통한 Rotation에 대한 이해 본문
공격 판정을 위한 Collision 설정을 위해 Capsule 모양의 Component를 Rotation Matrix를 사용하여 Rotate 시킬 일이 있어 이번에는 Rotation Matrix에 대해 더 자세히 알아보려 한다
우선 언리얼엔진에서 좌표는 앞이 X, 오른쪽이 Y, 위가 Z로 설정되어 있다. (음의 방향은 각각 뒤, 왼쪽, 아래)
구현할 예시는 아래와 같은 캡슐 모양을 Pawn이 향하는 방향으로 눕혀 공격 판정을 위한 Collision을 만드는 것이다.

이를 구현하기 위한 코드 중 Rotation을 담당하는 부분은 아래와 같다.
FVector TraceVec = GetActorForwardVector() * AttackRange;
FQuat CapsuleRot = FRotationMatrix::MakeFromZ(TraceVec).ToQuat();
GetActorForwardVector는 크기가 1인 Actor의 방향을 나타내는 Vector를 반환하는 함수이므로 여기에 공격 범위(사거리)인 AttackRange 값을 곱하면 Pawn이 바라보는 방향과 AttackRange의 크기를 가진 벡터가 반환된다.
AttackRange를 200으로 설정하고 TraceVec의 값을 확인해 보니 아래와 같다.
TraceVec: (103.278600 171.270344 0.000000)
Vector의 크기를 구해보면 반올림, 부동소수점 등에 의한 오차를 제외하면 200에 매우 가까운 것을 볼 수 있다.

다음으로는 FRotationMatrix namespace의 MakeFromZ 함수에 대해 알아보자.
언리얼엔진 공식문서에는 아래와 같이 간략하게 설명되어 있다.
Builds a rotation matrix given only a ZAxis.
Builds a rotation matrix given only a ZAxis. X and Y are unspecified but will be orthonormal. ZAxis need not be normalized.
Z축을 기반으로 회전행렬을 만들어서 반환하는 함수로 보이는데 내부 코드를 이어서 확인해 보겠다.
// RotationMatrix.h
template<typename T>
TMatrix<T> TRotationMatrix<T>::MakeFromZ(TVector<T> const& ZAxis)
{
TVector<T> const NewZ = ZAxis.GetSafeNormal();
// try to use up if possible
TVector<T> const UpVector = (FMath::Abs(NewZ.Z) < (1.f - UE_KINDA_SMALL_NUMBER)) ? TVector<T>(0, 0, 1.f) : TVector<T>(1.f, 0, 0);
const TVector<T> NewX = (UpVector ^ NewZ).GetSafeNormal();
const TVector<T> NewY = NewZ ^ NewX;
return TMatrix<T>(NewX, NewY, NewZ, TVector<T>::ZeroVector);
}
앞서 설정한 TraceVec: (103.278600 171.270344 0.000000)을 Input으로 line by line으로 값을 확인하면서 함수를 파악해 보자.
TVector<T> const NewZ = ZAxis.GetSafeNormal();
Input을 Unit Vector로 Normalize하는 함수다. (내부에는 연산 편의, 부동소수점으로 인한 값 소실 문제 처리가 되어있다)
벡터의 크기로 각 element를 나누면 아래의 값을 얻을 수 있다.
이를 새로운 Z축이라는 변수명으로 추정되는 NewZ로 이름 붙인다.
NewZ: 0.516393 0.856352 0.000000
TVector<T> const UpVector = (FMath::Abs(NewZ.Z) < (1.f - UE_KINDA_SMALL_NUMBER)) ? TVector<T>(0, 0, 1.f) : TVector<T>(1.f, 0, 0);
UpVector를 새로 세팅하는 코드다. UE_KINDA_SMALL_NUMBER는 1.e-4f로 설정되어 있다.
NewZ의 Z축 방향의 절댓값이 1과 매우 가까우면 (1,0,0)을 UpVector로 그렇지 않으면 (0,0,1)을 UpVector로 설정한다.
NewZ의 Z축 값이 0이기 때문에 UpVector는 (0,0,1)로 설정된다.
UpVector: (0,0,1)
const TVector<T> NewX = (UpVector ^ NewZ).GetSafeNormal();
NewX는 UpVector와 NewZ의 외적의 Unit Vector이다.
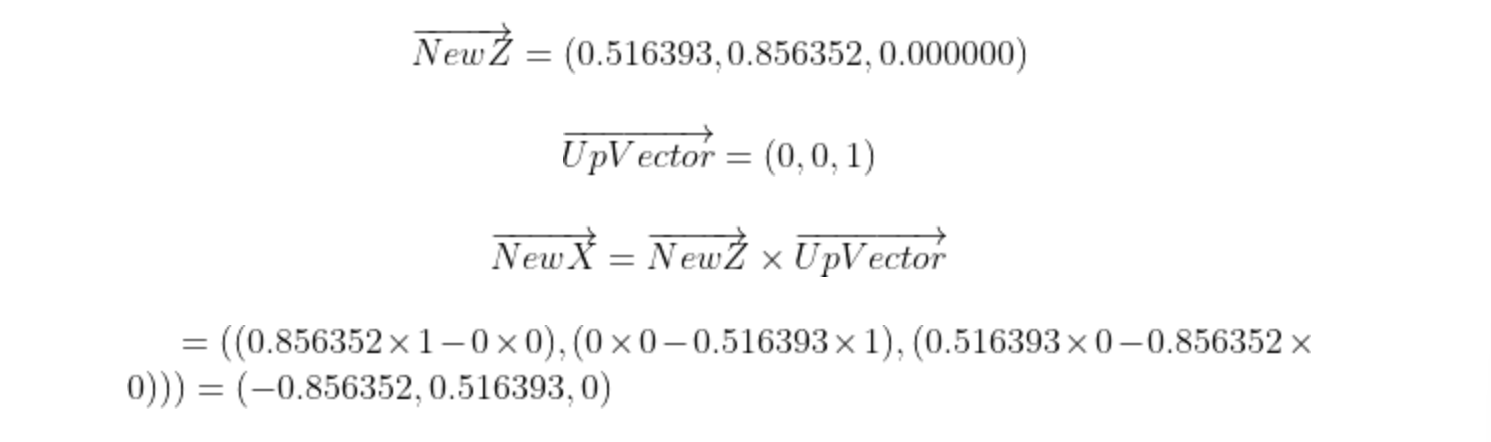
NewX: -0.856352 0.516393 0.000000
NewX는 외적이므로 UpVector와 NewZ가 Span하는 Plane의 Normal Vector이다.
그려서 확인해보면 NewX(노란색), UpVector(빨간색), NewZ(파란색)을 그려보면 아래와 같다.
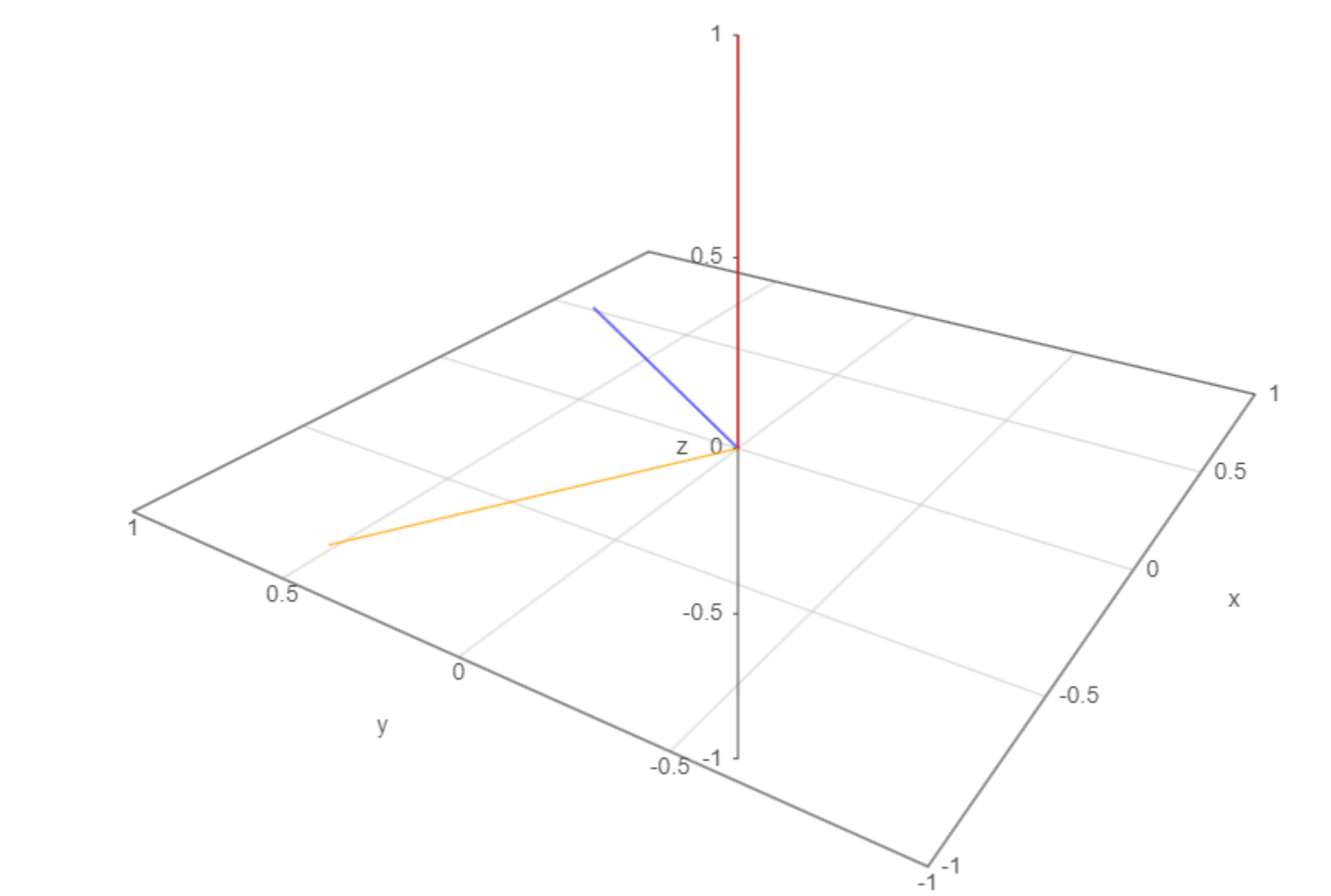
const TVector<T> NewY = NewZ ^ NewX;
NewX와 NewZ를 외적하여 두 벡터가 Span하는 평면의 Normal Vector인 NewY를 구한다.
NewX와 NewZ가 Span하는 평면의 식이 Z=0이기 때문에 Z축 방향의 벡터가 Normal Vector이자 NewY가 된다.
NewY: 0.000000 0.000000 1.000000
return TMatrix<T>(NewX, NewY, NewZ, TVector<T>::ZeroVector);
마지막으로 NewX, NewY, NewZ, Zero Vector를 사용하여 만든 Rotation Matrix를 반환한다.
MakeRotFrom(X or Y or Z) 함수는 아래와 같이 Rotator로 변환하여 반환시킨다.
return FRotationMatrix::MakeFromY(Y).Rotator();
예시로 든 TraceVec이 코드에서 임의로 설정하는 UpVector와 바로 직교하여 계산이 간단해졌지만 정리해보면
FRotationMatrix::MakeFromZ는
1. 인자로 받은 Vector를 Unit Vector로 정규화한 NewZ
2. NewZ의 Z-axis 절댓값에 따라 임의로 고른 UpVector(Z-axis Unit Vector 또는 X-axis Unit Vector)와 NewZ를 외적한 값을 정규화한 NewX
3. NewZ와 NewX를 외적하고 정규화하여 얻은 NewY
위 3개의 Unit Vector를 기저벡터로 하는 새로운 선형공간으로의 Linear Transformation을 수행하는 Rotation Matrix를 반환하는 함수다.
MakeFromX, MakeFromY는 각각 Input Vector가 X, Y축이 되도록 Linear Transformation하는 Rotation Matrix를 반환하는 함수임을 알 수 있다.
다시 구현예시인 "공격 판정을 위한 CapsuleComponent를 Pawn이 향하고 있는 방향으로 Rotate 시키기"를 생각해보면
Pawn이 바라보고 있는 방향이 새로운 Z축이 되기 때문에 Capsule모양의 Component가 우뚝 선 상태에서 캐릭터가 보는 방향으로 누운 모양이 될 것이라고 생각할 수 있다.

Reference
[0] MIT 18.06 Linear Algebra, Spring 2005 Instructor: Gilbert Strang
[1] 이득우의 언리얼 C++ 게임 개발의 정석
'Game Development > Unreal Engine' 카테고리의 다른 글
| [UE5] Revision Control - Git (0) | 2024.05.15 |
|---|---|
| [UE5] Behavior Tree로 순찰, 추적 AI 만들기 (0) | 2024.05.11 |
| [UE5] Delegate(델리게이트) (0) | 2024.05.08 |
| [UE5] Animation Retargeting(애니메이션 리타게팅) (0) | 2024.05.06 |
| [UE5] Enhanced Input(향상된 입력) (0) | 2024.05.04 |




