| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- 딥러닝
- dl
- NLP
- GAN
- WBP
- ddpm
- animation retargeting
- 디퓨전모델
- WinAPI
- Stat110
- Few-shot generation
- 언리얼엔진
- RNN
- Generative Model
- Unreal Engine
- Diffusion
- ue5.4
- 폰트생성
- BERT
- UE5
- multimodal
- 생성모델
- cv
- 오블완
- 모션매칭
- Font Generation
- CNN
- deep learning
- userwidget
- motion matching
- Today
- Total
Deeper Learning
Community Detection 본문
Community
군집(Community)은 집합에 속하는 정점 사이에 많은 간선이 존재하지만 집합에 속하는 정점과 그렇지 않은 정점 사이에는 적은 수의 간선이 존재하는 정점들의 집합이다.
Community Detection
그래프를 여러 군집으로 잘 나누는 문제를 군집 탐색(Community Detection) 문제라고 한다.
Configuration Model(배치 모형)

군집탐색의 metrics은 Modularity(군집성)을 사용한다.
군집성을 계산하는 수식은 다음과 같다.
S는 모든 군집 s의 집합

즉, 군집성은 무작위로 연결한 배치 모형과의 비교를 통해 통계적 유의성을 판단한다.
-1 이상 1 이하의 값을 가지며 보통 0.3 ~ 0.7 정도의 값을 가질 때 통계적으로 유의미한 군집을 찾아냈다고 말한다.
Girvan-Newman Algorithm
Girvan-Newman 알고리즘은 Top-down 방식의 군집 탐색 알고리즘이다.
간선을 순차적으로 제거하며 군집을 탐색한다.

군집을 분리하기 위해서는 위의 파란 부분과 같이 다른 군집을 연결하는 Bridge 역할을 하는 간선을 제거하여야 한다.
Bridge 역할을 하는 간선은 Betweenness Centrality(매개 중심성)을 통해 찾아낼 수 있다.
간선의 매개 중심성은 해당 간선이 정점 간의 최단 경로에 놓이는 횟수를 의미한다.

매개 중심성이 가장 높은 간선을 순차적으로 제거하면서 군집성을 기록하고 간선이 모두 제거되었을 때 군집성이 가장 높았을 때의 그래프를 복원하고 복원된 그래프의 연결 요소를 군집으로 정의한다.
Louvain Algorithm
Louvain 알고리즘은 반대로 Bottom-up 방식의 그래프 군집 탐색 알고리즘이다.
Louvain 알고리즘을 사용한 군집 탐색은 다음과 같은 방식으로 진행된다.
- 개별 정점은 모두 크기가 1인 군집으로 설정된다.
- 각 정점은 기존 혹은 새로운 군집으로 이동한다. 군집성이 최대화되도록 군집이 결정된다.
- 더이상 군집성이 증가하지 않을 때까지 2의 과정을 반복한다.
- 각 군집을 하나의 정점으로하는 군집 레벨의 그래프를 얻은 뒤 3을 다시 수행한다.
- 한 개의 정점이 남을 때 까지 4를 반복한다.

중첩 군집 탐색
위의 알고리즘들은 군집간의 중첩이 없다는 가정이 필요하다.
중첩이 있는 군집의 탐색 방법은 중첩 군집 모형을 찾아내는 과정과 같다.
중첩 군집 모형은 아래와 같이 가정한다.
- 각 정점은 여러개의 군집에 속할 수 있다
- 각 군집 A에 대하여, 같은 군집에 있는 정점은 $P_{A}$확률로 간선으로 직접 연결된다.
- 두 정점이 여러군집에 동시에 속할 경우 간선 연결 확률은 독립적이다.
- 어느 군집에도 속하지 않은 두 정점은 낮은 확률 epsilon으로 직접 연결된다.
중첩 군집 모형으로 그래프의 확률을 구할 수 있게 된다.
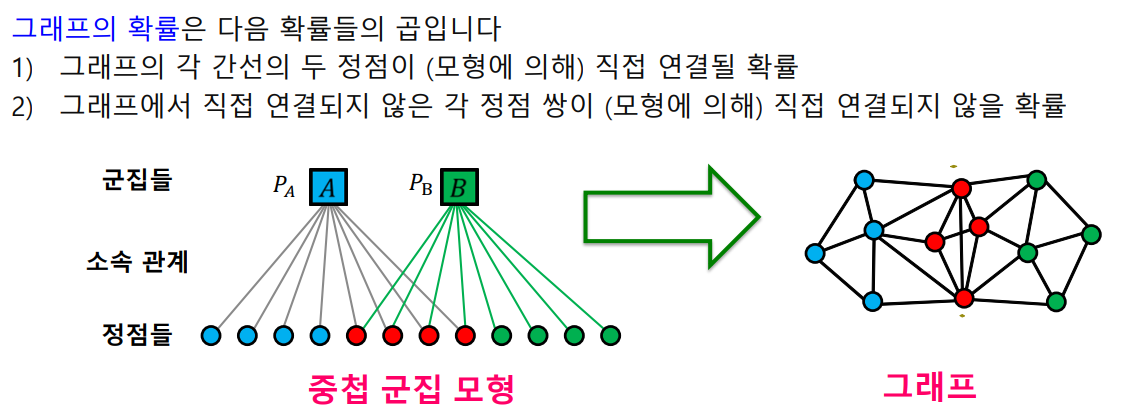
실제 간선으로 이어진 정점의 경우, 중첩 군집 모형이 이를 연결해 줄 확률
그렇지 않은 경우, 중첩 군집 모형이 이를 연결하지 않을 확률
이 둘을 모두 곱하여 그래프의 확률을 계산한다.
그래프의 확률을 최대화하는 중첩 군집 모형을 찾는 것이 중첩 군집 탐색이다.
중첩 군집 탐색을 용이하게 하기 위해 완화된 중첩 군집 모형을 사용한다.

완화된 중첩 군집 모형은 각 정점이 군집에 속해있는 정도를 실수 값으로 나타내어 경사 하강법과 같은 방식으로 모형을 탐색할 수 있는 장점이 있다.
'Statistics & Math' 카테고리의 다른 글
| [Statistics 110] 확률변수와 확률분포 (0) | 2022.03.27 |
|---|---|
| Eigenvector & Eigenvalue (0) | 2021.07.20 |
| PageRank (0) | 2021.02.24 |
| Graph (0) | 2021.02.23 |
| Bayes' theorem Introduction (0) | 2021.02.01 |




