Floating Point

Why Floating Point (부동 소수점)

 

Fixed point / Floating point

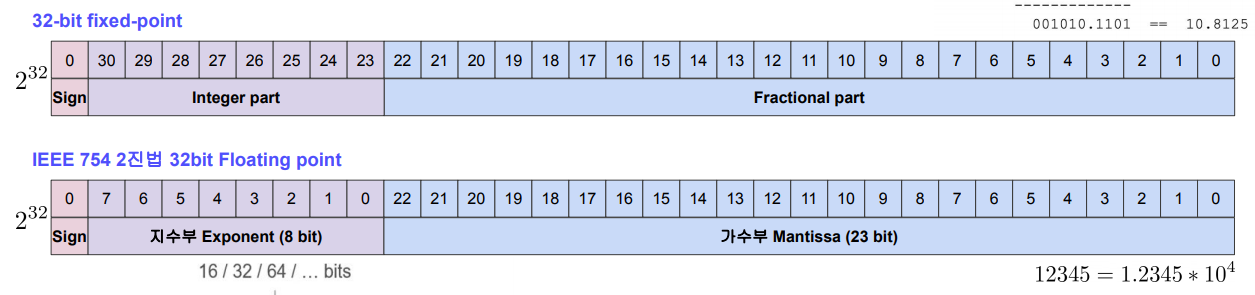
32bit는 총 2^32개의 수의 표현이 가능하다.

 

Fixed-point를 사용할 경우 정수부와 소수부의 bit 수가 고정이 되어 소수부가 모두 0인 정수의 경우 Fractional part의 bit가 모두 0을 나타낸다. 

이처럼 사용하지 않는 bit가 많아 비효율적이고 전체 표현가능한 수의 범위 또한 작다.

 

Floating-point를 사용할 경우 Fixed-point 처럼 표현 가능한 수가 연속적이지 않아 근사를 사용한다. 

정확도가 Fixed-point 보다 낮고 연산 속도가 느리지만 더 넓은 범위의 수를 표현할 수 있게 된다.

 

IEEE standard 754

IEEE 754는 IEEE에서 개발한 부동소수점을 표현하는 가장 널리 쓰이는 표준이다.

+0, -0, NaN, inf 등 기호의 표현과 연산이 정의되어있으며 32 bits (single-precision), 64 bits (double-precision), 80 bits (Extended-precision) 등의 형식이 있다.

 

n-bits precision (http://rvelthuis.de/articles/articles-floats.html)

위의 사진에서 빨간색 부분은 Sign bit를 나타낸다. 

Sign bit는 부호를 나타내는 bit로 양수의 경우 0, 음수의 경우 1의 값을 가진다.

 

노란색 부분은 지수 부분 (Exp, exponent)이며 파란색 부분은 가수 부분(fraction, Mantissa)이다.

 

Normalized Single precision example

 

Single precision

E = Exp-bias

M = 유효숫자

s = sign bit

이라고 할 때 위의 수식과 같은 꼴로 정의된다.

 

Float 15213.0을 부동소수점 형태로 나타내는 과정은 다음과 같다.

 

1) 10진수로 표현된 15213.0을 2진수로 변환한다.

 

 

2) 1.xxx의 형태로 만들기 위해 2의 n승을 곱해준다. E는 여기서 n이 된다. (E = 13)

 

 

 

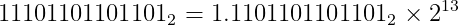
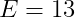
3) 유효숫자 M은 식에서 2의 거듭제곱을 곱한 부분을 제외한 2진수로 표현된 부분이며 Frac은 유효숫자의 소수점 아래 부분과 같다. (single-precision은 23bit를 Frac으로 사용하기 때문에 남은 bit는 0으로 채운다)

 

 

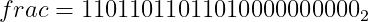
4) bias는 2^(k-1) - 1, Exp = E + bias (k는 지수부에 할당된 bit의 수로 single-precision에서 8이다. bias는 Exp가 음의 값을 가지지 않도록 해준다)

 

 

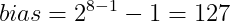
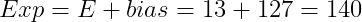
5) sign bit, Exp, Frac 순으로 비트를 나열하여 완성한다. ( 처음 수식에 따름 ) 

 

 

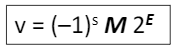
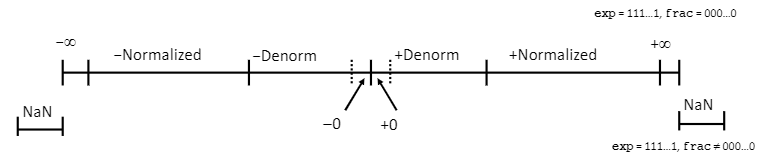
Denormalized, Special Values

Exp가 모두 0인 값은 Denormalized value, Exp가 모두 1인 값은 Special Values라고 한다.

 

Exp가 모두 0이며 frac이 모두 0인 Denormalized value는 0을 나타낸다.

sign bit에 따라 +0.0 , -0.0으로 표현된다.

 

Exp가 모두 0이고 frac이 0이 아닌 값들은 0에 매우 가까운 값을 나타낸다.

 

Exp가 모두 1인 수는 특별한 값을 나타내며 frac이 모두 0인 Special Value는 Infinity를 나타낸다.

마찬가지로 sign bit에 따라 +inf, -inf로 표현이 가능하다.

 

 

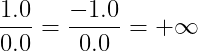
Exp가 모두 1이고 frac이 모두 0이 아닌 값은 NaN (Not - a Number)의 부동소수점 표기다.

numeric value로 정의되지 않는 값을 표현한다.

 

 

visualization

 

0.1 + 0.2 != 0.3

 

 

0.1+0.2는 0.3이 아니다.

 

 

Python의 자료형인 float은 double-precision이며 64bit로 수를 표현한다.

0.1과 0.2는 정확히 그 값이 아니며 근사한 수치의 값을 사용한다.

 

0.1 to floating point (double-precision) [S M Exp]

0.2 to floating point [S - M - Exp]

0.1 + 0.2

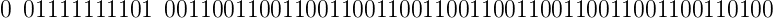
지수부를 나타내는 E의 스케일을 M의 조정을 통해 맞춰주고 bit 연산을 하고 반올림 등을 통해 bit 수를 다시 복구시켜주면 맨 아래 수와 같은 결과가 나온다. 

이는 십진수로 0.30000... 004의 값이다.

 

Reference

[1] betterprogramming.pub/why-is-0-1-0-2-not-equal-to-0-3-in-most-programming-languages-99432310d476

[2] Naver Boostcamp AI-Tech 모델 경량화 - 홍원의 강사