[Statistics 110] Lecture 29: Law of Large Numbers and Central Limit Theorem

Law of Large Numbers(큰 수의 법칙)

$X_1,...,X_n$이 i.i.d 이며 평균 $\mu$, 표준편차 $\sigma^2$일 때, 표본평균 $\bar X_n = \frac1 n\sum_{j=1}^{n}X_j$라고 정의

Strong LLN: n이 무한으로 가면 1의 확률로 $\bar X_N$ 이 $\mu$로 간다. (표본평균이 모평균에 근사)

Weak LLN: 모든 c>0에 대해 n이 무한으로 가면, $P(|\bar X_n - \mu| > c) \rightarrow 0$.

체비셰프 부등식을 활용한 Weak LLN 증명

$\bar X_n-\mu$가 0으로 수렴한다는 것은 알지만, $\bar X_n$ 분포에 대한 정보는 아직 알 수 없음

무한으로 가는 무언가와 곱하여 힌트를 얻을 수 있음 ($n^3$을 곱하였을 때 무한이 되거나 0이 되는것을 관찰하고 얼마나 빠른 속도로 $\bar X_n$이 $\mu$에 수렴하고 있는지 확인)

Central Limit Theorem(중심극한정리)

Normal Approximation to Binomial

$X \sim Bin(n,p)$, $X = \sum^n_{j=1} X_j, X_j \sim Bern(p) \space i.i.d .$

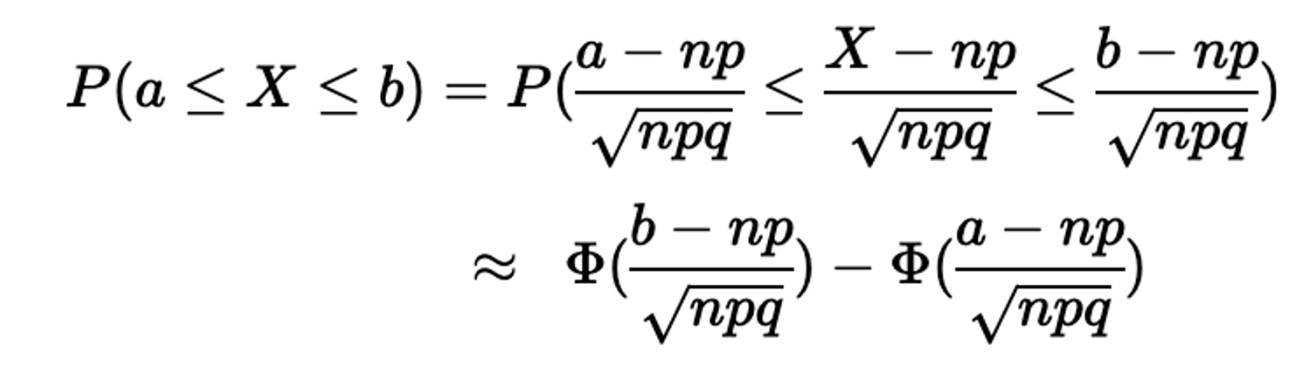
p가 1/2에 가깝고 n이 클 때 정규분포로의 근사가 빠르게 이루어짐 (포아송분포로의 근사는 p가 작을 때 용이)

 

Reference

[0] https://www.youtube.com/playlist?list=PL2SOU6wwxB0uwwH80KTQ6ht66KWxbzTIo