| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- motion matching
- WinAPI
- 생성모델
- multimodal
- BERT
- Generative Model
- 오블완
- Diffusion
- 디퓨전모델
- Stat110
- 모션매칭
- Unreal Engine
- dl
- 딥러닝
- cv
- NLP
- Font Generation
- UE5
- animation retargeting
- ue5.4
- userwidget
- 언리얼엔진
- GAN
- deep learning
- ddpm
- WBP
- Few-shot generation
- RNN
- CNN
- 폰트생성
- Today
- Total
Deeper Learning
SVM: Support Vector Machine (1) 본문
Support Vector Machine

빨간점, 녹색점이 각각 negative, positive class이며 feature의 dimension이 2인 데이터를 나타낸 그림이 있다. 성능이 좋은 분류모델의 Decision boundary를 그린다고 하면 보통 위의 실선을 그리게 될 것인데 이 때, 경계 주변의 점들이 주로 decision boundary의 개형을 결정하게 된다.
이를 모델링 한것이 Support vector machine이다 (이하 SVM)
Separate Hyperplane Constraints
위의 예시는 2차원으로 class를 나누는 경계인 hyperplane이 line으로 표현되며, 3차원에서는 plane이 hyperplane이 될 것이다. SVM의 목표는 데이터를 잘 분류할 수 있는 데이터의 차원보다 한 차원 낮은 차원의 subspace(d-1개의 linear independent한 벡터들이 span하는 space) hyperplane을 찾는 것이다.
n차원의 hyperplane을 정의하는 수식은 다음과 같다
β0+β1x1+β2x2+...+βnxn=0β0+β1x1+β2x2=wx+b=0
위의 두번째 수식처럼 내적을 사용하여 나타내는것이 가능하다. (2d이므로 직선)
직선 위에 존재하는 데이터 포인트를 positive case, 직선 아래에 존재하는 데이터 포인트를 negative case라고 하고 positive case의 label을 1로, negative case의 label을 -1로 생각해보자.
positive case에서는 wx+b>0, negative case에서는 wx+b<0 이 되며 이를 하나의 식으로 정리하면 아래와 같다.
y⋅(wx+b)>0
완벽하게 positive case와 negative case를 분류할 수 있는 decision boundary는 위 식을 만족해야만 한다.
Margin
margin은 decision boundary인 hyperplane의 모든 데이터 포인트와의 perpendicular distance 중 가장 작은 distance이다.
위 그림에서 3개의 separate hyperplane에서 가장 아래에 있는 직선은 바로 하단 빨간점과 거리가 매우 가까우며 가장 상단에 있는 직선은 바로 위쪽의 초록점과 매우 가까이있다. 그 사이에 위치한 직선이 가장 작은 margin distance를 가지고 있으며 margin distance을 고려한다면 더 좋은 hyperplane이라고 할 수 있다.
이제 margin distance를 구하는 수식에 대해 알아보겠다.
decision boundary의 수식을 f(x)=wx+b 라고 하면 decision boundary 위의 점에서 f(x)=0 이 되고 positive point에서는 식의 값이 양수인데, 이를 임의의 양수 a라고 생각해보자. f(x)=a,(a>0).
지정한 positive point를 x, x에서 decision boundary에 수선을 내려 생긴 교점을 xp 라고 하고 margin distance를 r 이라고 해보자.

Perpendicular w
decision boundary에 수직인 unit vector는 w||w|| 이므로 아래처럼 식을 쓸 수 있다.
x=xp+rw||w||
w가 decision boundary에 perpendicular한 이유는 hyperplane의 수식을 wx+b=0 으로 정의하였기 때문에 wx=−b 라고 할 수 있다. 양변에 상수를 곱해 w 를 크기가 1인 unit vector로 만들었다고 가정하자. w 가 unit vector일 때 b 는 origin과 hyperplane의 perpendicular distance와 같다.
origin에서 hyperplane 위에 위치한 임의의 point까지 이어 벡터를 만들면 그 벡터와 w 의 dot product은 −b 가 되어야 한다. (wx=−b).
w가 unit vector이기 때문에 dot product 값은 scalar projection 값과 동일하며 x를 w 에 projection한 벡터의 길이가 b 와 같으려면 w 는 hyperplane과 perpendicular한 vector여야만 한다.
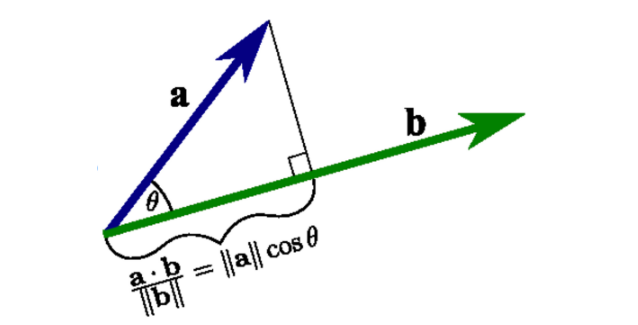
w is perpendicular to hyperplane: https://stackoverflow.com/questions/10177330/why-is-weight-vector-orthogonal-to-decision-plane-in-neural-networks
scalar projection, vector projection: https://flexbooks.ck12.org/cbook/ck-12-college-precalculus/section/9.6/primary/lesson/scalar-and-vector-projections-c-precalc/
margin distance calculation
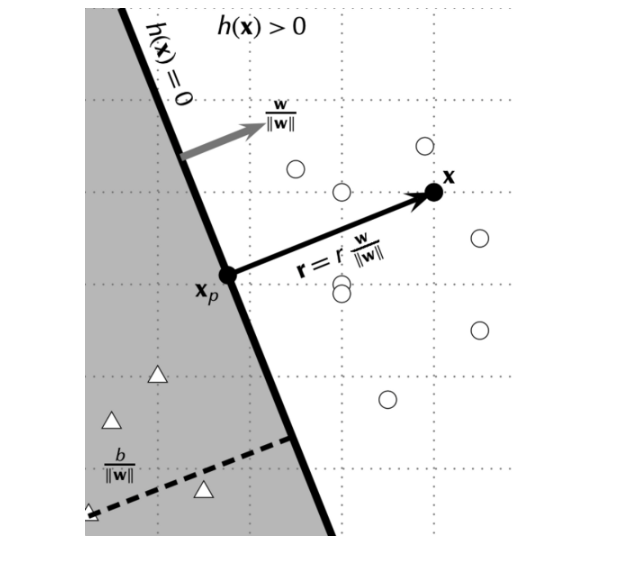
이제 위 그림에서 w||w|| 가 hyperplane에 perpendicular 하다는 것을 확인하였으니 이어서 margin distance r 을 계산해보겠다.
x=xp+rw||w||
xp 는 hyperplane 위에 있기 떄문에 wxp+b=0. 이제 식을 쭉 전개해보면
f(x)=wx+b=w(xp+rw||w||)+b=0+rww||w||=r||w||r=f(x)||w||=a||w||(positive)
margin distance를 maximize 하여야 좋은 decision boundary를 가질 수 있도록 하는것이 중요하다. positive case, negative case 양쪽 margin을 모두 고려해서 식을 아래와 같이 정리할 수 있다.
max
a는 앞서 정한 임의의 양수로 maximize 식에서는 1로 대체하고 이를 minimize 식으로 바꾸면
\min_{w,b}r= {||w||} \\ s.t. (wx_j+b)y_j \ge 1, \forall j
w는 w_1,w_2 로 구성되어 있어 ||w|| = \sqrt{w_1^2+w_2^2} 을 minimize하여야 되므로, Quadratic Programming을 활용하여 optimize한다. (더 상세한 내용은 https://towardsdatascience.com/support-vector-machines-dual-formulation-quadratic-programming-sequential-minimal-optimization-57f4387ce4dd 참고)
Q. (wx_j+b)y_j \ge 1, \forall j 에서 1로 a 를 설정하는 이유는?
- wx+b 가 0 이상이면 positive, 0 이하면 negative로 분류할 수 있는 hyperplane은 무한정 많기 때문에 각각 positive, negative support vector를 지나는 두 평행한 hyperplane을 정의하기 위해 \pm \delta 값을 사용하여 wx+b = \pm\delta 와 같이 설정할 수 있다. \delta 자체를 새로운 학습가능한 parameter로 설정하기보다는 w,b 에 대한 최적화를 수행하는 것이 편리하기 때문에 수학적 편의를 위해 \delta 를 1로 설정하여도 무방하다
Inseparable case
가까운 positive, negative 데이터 포인트를support vector로 정하고 margin을 최대화 하는 방식으로 hyperplane을 지정할 수 있다.
이러한 방식이 항상 잘 작동하는가에 대해서는 의문이 있는데 현실 세계에서는 데이터에 noise가 내재되어 있기 때문이다. 2차원 데이터에서 하나의 negative 데이터 포인트라도 positive 데이터 포인트 주변에 위치한다면 지금까지 다룬 에러케이스를 허용하지 않는 Hard margin으로는 optimization이 정상적으로 작동하지 않는다.
optimize된 hyperplane이 데이터를 완전히 구분할 수 없는 inseparable 문제를 해결하기 위해 Soft margin, Kernel trick을 사용한다.
Soft margin SVM
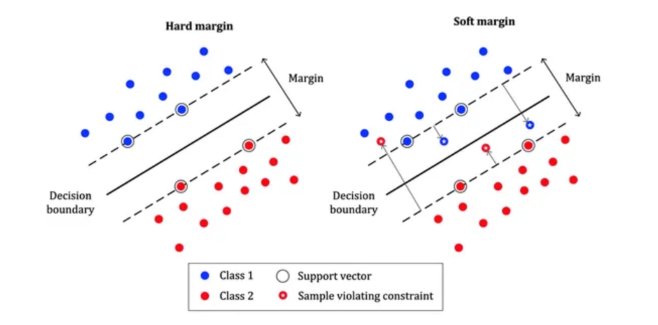
https://miro.medium.com/v2/resize:fit:1104/format:webp/1*CD08yESKvYgyM7pJhCnQeQ.png
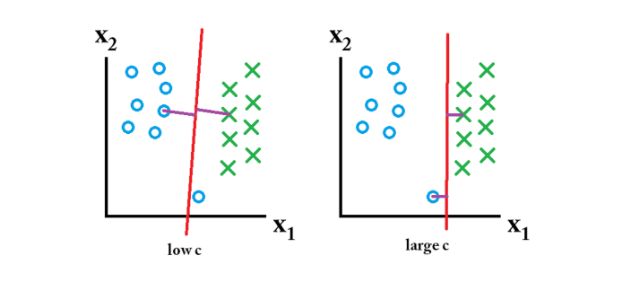
우측의 그림은 Soft margin을 사용하였을 때 decision boundary이다. 몇몇 데이터가 negative case임에도 positive case 주변에 위치하였음에도 그럴듯한 decision boundary를 그려냄을 볼 수 있다.
Soft margin은 에러를 허용하지 않는 Hard margin과 다르게 에러를 허용하고 대신 그에 따른 penalization을 주는 방식이다.
이를 최적화 수식에 어떻게 반영할까? 먼저 에러 개수에 따라 penalize 한다고 하면 식은 아래와 같다.
\min_{w,b} {||w||}+C \times \#_{error} \\ s.t. (wx_j+b)y_j \ge 1, \forall j
위 식은 에러 케이스의 개수에 계수 C 를 곱해 penalize하는 방식으로 식을 minimize 하기 위해서는 더해지는 error penalize 항을 최소로 만들어야한다.
이 방식에도 문제가 있는데 에러의 정도를 반영하지 않으며 수식 자체도 quadratic optimization에 잘맞지 않다는 것이다.
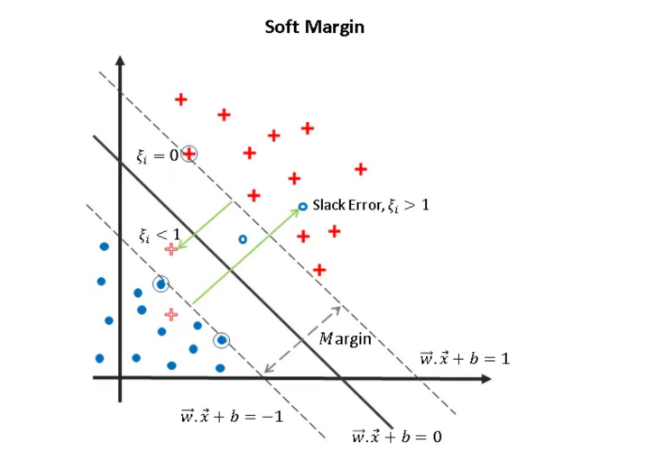
대신 일반적으로 데이터 포인트의 class의 hyperplane(위 그림에서는 점선)과의 margin distance인 slack variable \xi 를 도입한 식을 사용한다.
\min_{w,b} {||w||}+C \times \sum_j \xi_j \\ s.t. (wx_j+b)y_j \ge 1-\xi_j, \xi_j \ge 0,\forall j,
Hard margin과 다르게 제약식이 각 데이터 포인트의 slack variable 만큼 완화시켜 decision boundary가 무조건 생길 수 있는 조건이 되었지만(hard margin에서는 inseparable한 infeasible case) 최적화 수식에서 마찬가지로 penalty를 부여한다.
C 값을 커지면 error case에 대한 penalty가 최적화 식에 미치는 영향이 커져 아래 그림처럼 error에 대한 penalty가 더 작아지도록 decision boundary가 형성된다. C 가 너무 작은 경우에는 데이터 포인트가 잘못된 위치에 있어도 penalty를 거의 받지 않기 때문에 정상적인 decision boundary가 형성되지 않는다.
다음 글에서는 이어서 dual problem, lagrange multiplier, kernel trick 등을 다루어보겠다
Reference
[1] https://ankitnitjsr13.medium.com/math-behind-svm-support-vector-machine-864e58977fdb
'AI > Machine Learning & Data Science' 카테고리의 다른 글
| 직관과 MLE, MAP(2) (0) | 2023.06.27 |
|---|---|
| 직관과 MLE, MAP (1) (0) | 2023.06.22 |
| MLE(Maximum Likelihood Estimation), MAP(Maximum A Posterior) (0) | 2022.11.25 |
| Generative modeling (0) | 2021.08.16 |
| Netflix Challenge - Recommendation System (0) | 2021.02.25 |



