| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- ue5.4
- Font Generation
- 폰트생성
- dl
- multimodal
- 디퓨전모델
- userwidget
- GAN
- BERT
- UE5
- Diffusion
- RNN
- WBP
- cv
- Few-shot generation
- 모션매칭
- Generative Model
- 언리얼엔진
- animation retargeting
- deep learning
- 딥러닝
- CNN
- motion matching
- ddpm
- Stat110
- 오블완
- Unreal Engine
- WinAPI
- 생성모델
- NLP
- Today
- Total
Deeper Learning
Glove 본문
Glove
Glove(Global Vectors for Word Representation)은 워드 임베딩을 구현하는 방법론으로 count와 prediction 2가지 방법을 모두 사용하는 알고리즘이다.
CBOW와 Skip-gram을 활용한 언어 모델에서는 Corpus 전체의 통계적 정보를 활용하지 않는다.
Word2Vec 임베딩으로는 local context가 유일한 단어를 임베딩 하는데 필요한 정보가 되기 때문에 문법적 영향으로 주변 단어가 동일한 단어군은 비슷한 벡터 공간에 매핑된다.
뜻이 다르더라도 주변 단어가 비슷한 경우는 작은 단위의 Corpus에 자주 나타나며 이렇게 임베딩 된 단어 벡터는 특정 과제를 수행할 때 문제가 있을 수 있다.
이러한 문제점은 local window와 함께 전역적인 정보를 함께 활용하는 Glove로 해결이 가능하다.
Co-occurrence probability
Corpus 전체에서 기준 단어 전후로 window size내에 위치한 단어가 있으면 이 두 단어는 Co-occurrence (동시발생)하였다고 말한다.
$X_{ij}$는 단어 i를 기준으로 window size내에 위치한 단어(Context word)에 j가 존재한 횟수를 나타낸다.
$X_{ij}$를 사용하여 단어 i와 j의 Co-occurrence probability를 다음과 같은 수식으로 구할 수 있다.


위 논문의 예시를 보면 solid의 경우 $P(solid|ice)$의 값이 $P(solid|steam)$의 값보다 큰 것을 볼 수 있다.
이는 ice가 등장할 때 solid가 등장할 확률이 steam이 등장할 때 solid가 등장할 확률보다 높다는 것이다.
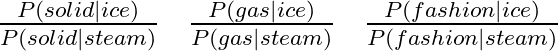
Co-occurrence probability의 비율을 살펴보자.
먼저 solid의 경우 ice와 관련이 크고 $P(solid|ice)$의 값이 더 크기 때문에 1보다 큰 값이 나온다.
gas는 steam과 관련이 크며 $P(gas|steam)$의 값이 더 커서 1보다 작은 값이 나온다.
fashion은 ice와 steam 모두 관련이 없어 1에 근접한 값을 가진다. (둘다 관련이 있을 경우에도 동일)
위를 통해 단어의 의미의 유사성을 표현하는 matrix를 얻을 수 있다.
Formula

w는 Word2vec에서와 마찬가지로 2개의 생성되는 input layer와 hidden layer사이의 weight matrix이다.
w'은 hidden layer와 output layer사이의 matrix로 w의 전치 행렬과 같은 형태를 가진다.
임베딩 된 벡터로 Co-occurrence prob ratio를 나타내기 위해 위와 같이 식을 보기 편하게 바꾸었다.
마지막에 $w_{i}-w_{j}$가 함수 F의 input으로 들어간 이유는 두 단어 사이의 비율은 임베딩 된 벡터 공간에서 다음과 같이 두 벡터의 차를 활용하여 나타낼 수 있기 때문이다.
Glove의 아이디어는 Word2vec과 같은 방식의 local window를 사용한 Embedding에 corpus 전체의 global 한 단어의 분포 정보를 추가하자는 것이다.
이는 Target word와 그 Context word의 내적이 전역적인 정보인 두 단어의 co-occurrence prob과 비례하도록 만드는 것이다.
위 식에서 $(w_{i}-w_{j})$와 $\frac{P_{ik}}{P_{jk}}$에서 보면 상대적인 관계는 -와 /에서 똑같이 유지되어야 하며 따라서 함수 F는 Homomorphism(준동형)을 만족시켜야 한다는 것을 알 수 있다.
준동형이란 모든 연산 및 관계를 보존하는 함수를 말한다.
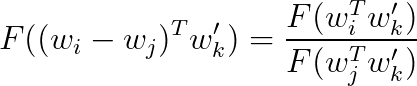
위와 같은 준동형 함수 F는 지수 함수로 제시된다.

양변에 로그를 사용하면 위 그림에서 아래 수식과 같은 형태가 된다.
i와 k가 바뀌어도 같은값을 반환하도록 수식을 변경하여야 한다. ( $-logX_{i}$ 의 값으로 인해 달라짐 )
이를 다른 학습 가능한 bias인 $b_{i}$, $b'_{k}$로 대체하여 식을 완성한다.




위와 같은 Loss function이 완성되며 여기서 $f(X_{ij})$는 I am과 같은 $X_{ij}$값이 높은 단어 쌍에 대하여 Loss를 조절하기 위해 알맞은 값을 가진다.
Reference
Jeffrey Pennington et al. (2014). 'Glove: Global Vectors for Word Representation' url
Thushan Ganegedara. Intuitive Guide to Understanding GloVe Embeddings. url
'AI > Deep Learning' 카테고리의 다른 글
| BLEU (Bilingual Evaluation Understudy Score) (0) | 2020.12.24 |
|---|---|
| Beam Search (0) | 2020.12.24 |
| Word2Vec (0) | 2020.12.06 |
| Inception score (IS) (0) | 2020.12.04 |
| Feature Extraction (0) | 2020.12.04 |




