| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- deep learning
- Generative Model
- CNN
- inductive bias
- userwidget
- 디퓨전모델
- multimodal
- Stat110
- GAN
- cv
- 언리얼엔진
- ddpm
- 모션매칭
- Diffusion
- animation retargeting
- dl
- WinAPI
- Unreal Engine
- RNN
- ue5.4
- BERT
- Font Generation
- 생성모델
- motion matching
- UE5
- 폰트생성
- WBP
- Few-shot generation
- NLP
- 딥러닝
- Today
- Total
Deeper Learning
Beam Search 본문
Why Beam Search?
기계번역, 이미지 캡션 생성 등 $\hat{y}$가 둘 이상의 연속적인 Sequence가 되는 Decoder 형태의 모델에서 예측된 값은 다음 예측을 위한 input 값으로 피딩 된다.

위의 예시에서 Greedy Search를 사용하면 빠른 속도로 예측 과정이 완료되나 하나의 예측만을 고려하기 때문에 minor 한 변화에 영향을 받지 않아 최적의 예측을 하지 못활 확률이 Beam Seach보다 높다.
따라서 여러가지 예측을 하는 Beam Search를 사용한다.
Beam Search

vocab size가 10000인 예시에서 Encoder 부분을 지나고 처음으로 예측이 이루어지는 부분에서 구해야 하는 값은 $\underset{y}{argmax}P(y^{<1>}|x)$이다. ($y^{<n>}$은 n번째 예측)
Beam width = 3 일때 $\underset{y}{argmax}P(y^{<1>}|x)$인 높은 순으로 3개 선정한다. ( softmax를 통해 구해진 확률 값)
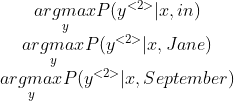
다음으로 고려할 확률은 위의 3개의 식과 같다.
in, Jane, September에서 각각 Beam width인 3개의 가장 확률이 높은 y를 선정한다.
in이 $y^{<1>}$ 일 때 vocab size가 10000개로 총 10000개의 확률 값, Jane과 September에서도 10000개씩 총 30000개의 확률값 중 가장 높은 3개를 선정한다.
이 과정을 y의 길이인 Ty (<EOS> 만나기 전까지의 길이)까지 반복을 한다.

첫 번째 식은 궁극적으로 구하고자 하는 확률 $P(Y|X)$이며 이는 조건부 확률로 두 번째 식과 같이 변환이 가능하다.
두 번째 식은 지금까지 구한 확률 값이 곱해진 형태로 세 번째 식의 형태로 축약이 가능하다.
3 번째 식의 값을 최대로 만드는 Y를 구하는 것이 궁극적인 목표와 같다. (Y는 y1, y2, y3,...,yt를 원소로 하는 list)
y의 길이가 길어지면 확률 값의 곱은 매우 작아지게 되므로 log 변환을 통해 이를 아래와 같이 수정한다.

log 변환이 이루어진 확률 값은 1보다 작아 음수이고 이를 모두 더하기 때문에 y의 길이가 길어지면 값이 작아지게 되고 모델은 짧은 기계번역 결과물을 선호하게 된다.
따라서 이를 위해 추가로 $(T_{y})^{a}$를 도입한다.
a의 값은 0에서 1 사이로 a를 조절하여 Normalize의 정도를 정한다.
a가 0일 때 1/1이 되어 1의 값이 곱해져 길이에 따른 Normalize를 적용하지 않는다.
a가 1일 때 y의 길이의 역수가 곱해져 길이에 따른 Noramalize의 정도가 최대가 된다.
Beam width가 1이면 Greedy Search와 동일하며 Beam width가 작으면 빠르고, 최적의 결과가 나올 확률이 비교적 낮다.
Beam width가 크면 가능한 예측의 개수가 많아져 시간이 오래 걸리지만 최적의 결과가 나올 확률이 비교적 높다.
Error Analysis
$y^{*}$을 최적의 기계번역 결과라고 하면 $P(y^{*}|x) > P(\hat{y}|x)$인 모델에서 Beam Search로 찾아낸 최적의 y가 $hat{y}$라면 이는 Beam Search에서 문제가 발생한 것으로 Beam width를 더 크게 설정하여 해결한다.
$P(y^{*}|x) <= P(\hat{y}|x)$ 이면 이는 RNN 모델에 문제가 있는 것으로 분석한다.
'AI > Deep Learning' 카테고리의 다른 글
| Deep Convolutional Generative Adversarial Networks (DCGAN) (0) | 2020.12.28 |
|---|---|
| BLEU (Bilingual Evaluation Understudy Score) (0) | 2020.12.24 |
| Glove (0) | 2020.12.08 |
| Word2Vec (0) | 2020.12.06 |
| Inception score (IS) (0) | 2020.12.04 |




