| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- ue5.4
- Stat110
- CNN
- 오블완
- 생성모델
- ddpm
- 언리얼엔진
- BERT
- 디퓨전모델
- WBP
- userwidget
- motion matching
- Few-shot generation
- Font Generation
- 모션매칭
- RNN
- deep learning
- NLP
- Diffusion
- UE5
- Unreal Engine
- dl
- cv
- 폰트생성
- GAN
- animation retargeting
- WinAPI
- 딥러닝
- Generative Model
- multimodal
Archives
- Today
- Total
Deeper Learning
Pixel-Adaptive Convolutional Neural Networks 본문
Abstract
- Convolutions은 CNN의 기본 building block
- spatially shared weights는 CNN이 쓰이는 이유임과 동시에 한계점이다
- learnable local pixel features에 따라 변하는 pixel-adaptive convolution(PAC)를 제시
- PAC는 자주 쓰이는 filter들의 일반화 버전으로 많은 case에서 그대로 사용이 가능하다.
- deep join image upsampling에서 SOTA
- fully-connected CRF를 PAC-CRF로 대체하여 성능, 속도 향상
- pre-trained networks에서 PAC drop-in replacement로 성능 향상
1. Introduction
- standard convolution의 두 특징의 단점을 개선: Spatial Sharing, Content Agnostic
- Spatial Sharing
- 기본 CNN은 전체 input에 대해 같은 filter를 사용하여 fc layer에 비해 parameters가 적음
- semantic segmentation 같은 dense pixel prediction task에서는 pixel grid에 따라 scene이 다르기 때문에 loss도 달라 gradient는 각 pixel에 대해 다른 방향으로 전달되는 것이 최적
- 하지만 CNN의 spatial sharing에 의해 filter에 대한 gradient는 globally pooled 되어 전달된다.
- 이로 인해 CNN의 필터는 전체 pixel에 대한 error를 줄이는 식으로 학습되며 이는 특정 location의 pixel grid에 대해서 sub-optimal solution이다.
- Content-Agnostic
- convolution filter는 학습이 완료되면 모든 image에 같은 filter를 사용한다.
- 모든 image type(e.g., sky vs. pedestrian pixels)에 대해 하나의 kernel weight가 optimal solution이 될 수는 없다
- 매우 많은 filter를 학습하여 image와 pixel variations을 커버 가능한 모델을 학습시킬 수 있지만 이는 매우 많은 memory와 labeled data를 필요로 한다.
- content-adaptive filter를 network에 포함시키는 것이 저자의 새로운 접근법
- 기존의 content-adaptive convolutional networks는 크게 두 타입으로 나눌 수 있다.
- Traditional image-adaptive filters
- bilateral filter
- 가우시안 필터의 경우 아래와 같이 grid에 대해 가우시안 함수를 곱하여 가우시안 노이즈를 제거하는데 효과적이나 edge가 흐려지는 문제가 있음

- 이를 보완하는 bilateral filter는 중심으로 부터의 Euclidean distance가 유일한 weight를 결정하는 factor가 되는 Gaussian filter와 달리 radiometric differences (range differences like color intensity, depth distance)가 weight를 결정하는 추가 factor가 되어 adaptive 한 filter가 생성된다.
- 가우시안 필터의 경우 아래와 같이 grid에 대해 가우시안 함수를 곱하여 가우시안 노이즈를 제거하는데 효과적이나 edge가 흐려지는 문제가 있음
- CNN의 result를 향상시킬뿐 standard convolution의 대체재가 아님
- bilateral filter
- learning position-specific kernels using a separate sub-network
- sub-network가 각 pixel의 convolution filter weights를 추론
- Dynamic Filter Networks(DFN)
- standard convolution을 대체할 수 있으나 전체 network에 사용하기에 large number of filter banks
- PAC는 DFN과 다르게 spatially invariant convolution filter W를 spatially varying filter K와 곱하여 커널을 만든다.
- adapting kernel K는 pre-defined form(Gaussian or Laplacian)과 pixel feature에 의해 결정된다.
- e−12||fi−fj||2,fi∈Rd fi 는 i번째 pixel의 d-dim feature
- f 는 adapting feature로 pixel-position이나 color로 pre-define 되거나 CNN을 통해 학습 또한 가능하다.
- PAC는 standard convolution에서 간단한 수정만 하였음에도 widely-used filter로 일반화되며 flexible
- PAC는 spatial convolution, bilateral filtering, pooling operations(avg pool, detail-preserving pooling)가 될 수 있는 일반화 성능이 좋은 convolution
- transposed convolution에 PAC를 사용하여 guided upsampling을 학습할 수 있다
2. Related Work
Image-adaptive filtering
- bilateral filtering
- guided image filtering
- non-local means
- propagated image filtering
Dynamic filter networks
- DFN - Jia et al.
- sensible architecture design
- difficult to scale to multiple dynamic-filter layers
- Deformable convolution - Dai et al.
- geometric-invariant features를 학습하기 위한 offset
Self-attention mechanism
- self-attention mechanism과 비슷한 개념
- global context & each location's response를 사용
- 전체 image에 attention 연산을 하는것은 computationally expensive, low-dimension feature map에 주로 사용
- PAC은 local context에 더 민감하며 계산적으로 효율적임
3. Pixel-Adaptive Convolution
- Standard spatial convolution
- spatial image features v=(v1,...,vn),vi∈Rc , n pixels, c channels
- filter weights W∈Rc′×c×s×s
- pixel coordinates pi=(xi,yi)T, Ω() = s x s convolution window

- 위 수식으로 standard spatial convolution을 나타낼 수 있다.
- pi−pj 는 input sampling pixel의 위치를 나타내는 부분으로 2D offset인 j를 iteration 하며 샘플링한다. (e.g. i = (3,3), j = ((-1,1),(-1,0),(-1,-1), ... , (1,-1)))
- 수식을 보면 weights가 오직 pixel position에 따라 결정되는 content-agnostic, spatially shared 성질을 확인할 수 있다.
- content-adaptive convolution operation
- pixel feature에 따라 W를 결정

- f∈Rd 이므로 input signal v는 d-dimensional space로 projection하여 f를 만들고 W와 d-dimensional convolution 연산이 필요하다.
- 이전의 high dimensional filtering은 Gaussian filter와 같은 hand-specified filter에 국한되었으나 최근 연구는 high-dimensional space에서 W를 학습하였다.
- 그러나 high-dimensional convolution은 몇몇 단점이 있음
- 고차원에 projection된 데이터는 sparse 하기 때문에 적절한 computational overhead를 위해서는 격자나 테이블 형식의 특별한 구조가 필요하다.
- f 를 학습하기가 어려워 hand-specified feature space (color, position)을 사용한다. (e.g. f = (x, y, r, g, b)
- 고차원에서 curse of dimensionality를 피하기 위해 feature의 dimension d에 제약이 걸린다.
- spatial sharing의 이점이 high-dimensional filtering에서 사라지게 된다.
- Pixel-adaptive convolution
- higher dimensions의 문제를 피하기 위해 spatially invariant convolution을 수정하는 방식

- spatially varying kernel K∈Rc′×c×s×s 는 pixel feature f 에 의해 결정된다
- K(fi,fj)=exp(−12(fi−fj)T(fi−fj)) 와 같이 pre-defined form (Gaussian)으로 정의되어 higher dimension으로의 projection 없이 2D grid 자체에서 filtering이 가능하다.
- pixel features f 를 사용하여 adaptive 하게 adapting kernel K 를 만들기 때문에 위 연산을 Pixel-Adaptive Convolution(PAC)라고 부른다.
- f 는 color features (x,y,r,g,b)로 설정할 수도 있으며 end-to-end로 learnable feature로도 설정이 가능하다.
- Generalizations
- standard convolution에서 조금의 변형만 하였음에도 널리 쓰이는 여러 filtering operations으로 일반화가 가능하다.

- DFN의 경우 auxiliary network를 사용하여 filter를 생성하여 PAC보다 제약이 적고 general
- PAC는 여러 layer에서 재사용 가능한 learned pixel embedding f 를 사용
- PAC는 spatial filter W와 adapting kernel K를 사용하여 filter를 factorization 하는 것과 비슷하며 이는 DFN의 문제인 hast table, 격자 구조의 강제를 줄이며 standard convolution의 문제인 non-adaptive kernel를 adaptive하게 구성하는 좋은 trade-off point를 사용
- Implementation and variants
- learnable deep features f
- Trasposed PAC
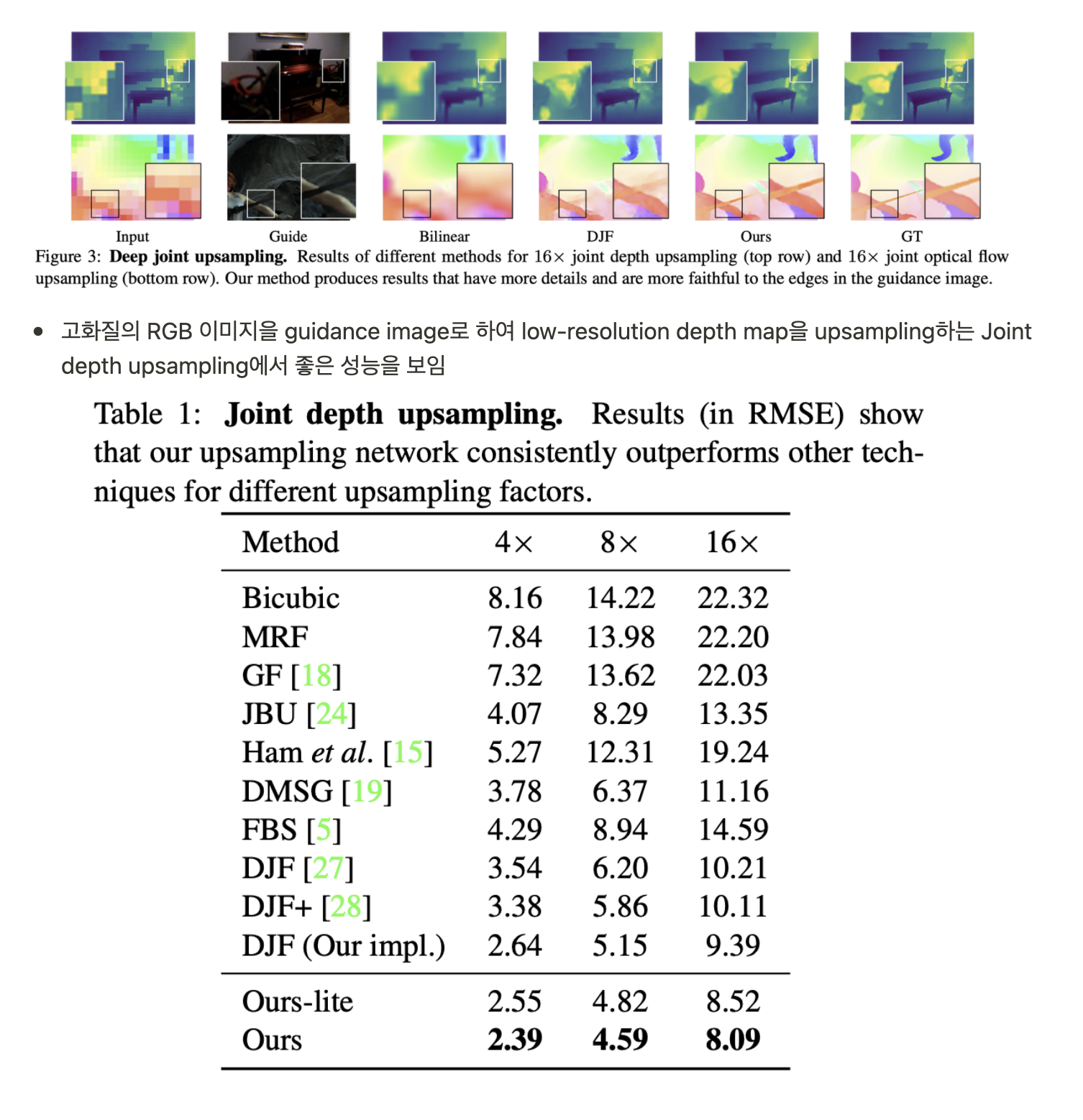
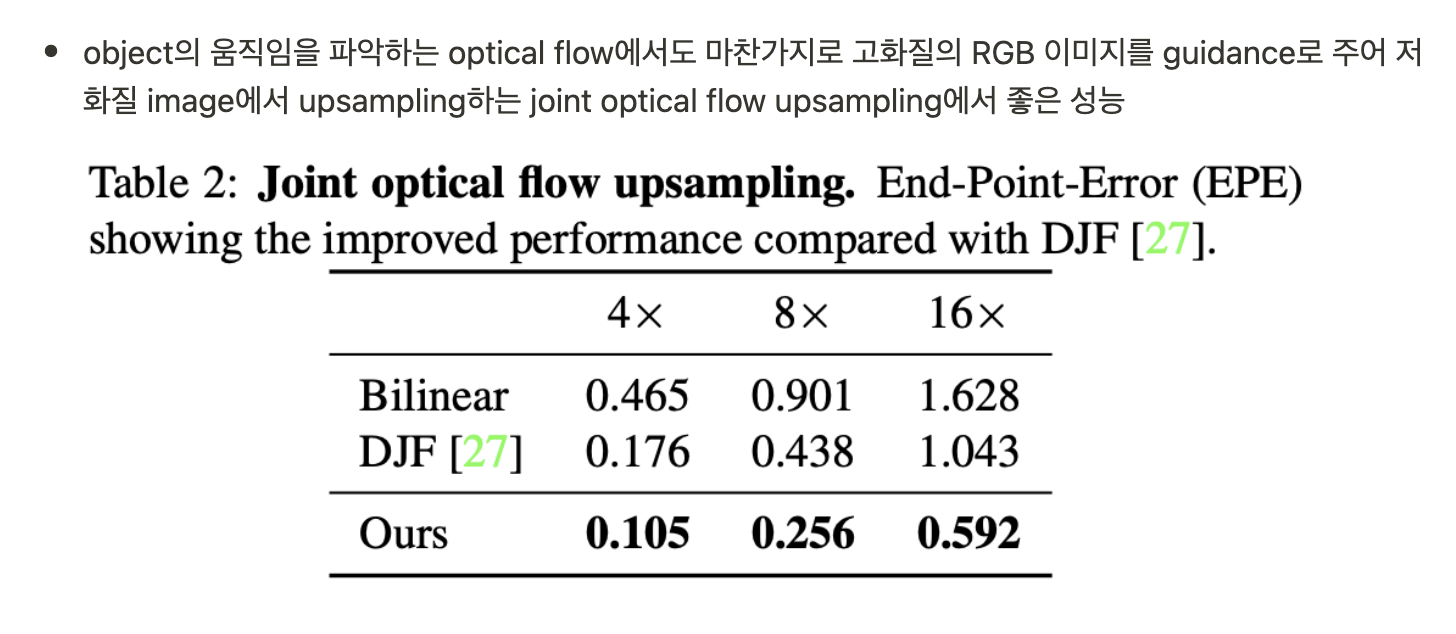
4. Deep Joint Upsampling Networks
- Joint upsampling은 저화질의 signal을 고화질의 guidance image를 사용하여 upsampling 하는 task
- 예시로 low-resolution depth map의 guidance로 고화질의 RGB 이미지를 제공
- PAC는 joint image processing에 필요한 적절한 filter를 guidance image에서 adapting feature를 사용하여 만든다
- Decoder의 Transposed PAC를 사용, adaptive kernel K는 Guidance branch에서 담당
5. Conditional Random Fields
- 컴퓨터 비전에서 CRF는 region-based approaches, short-range structure에 국한되어 있었다
- Full-Connected CRF(Full-CRF)는 픽셀 간의 dense connection을 통해 효율적인 추론을 위한 고차원 필터링을 하였다.
- PAC로 효과적이고 학습 가능한 CRF
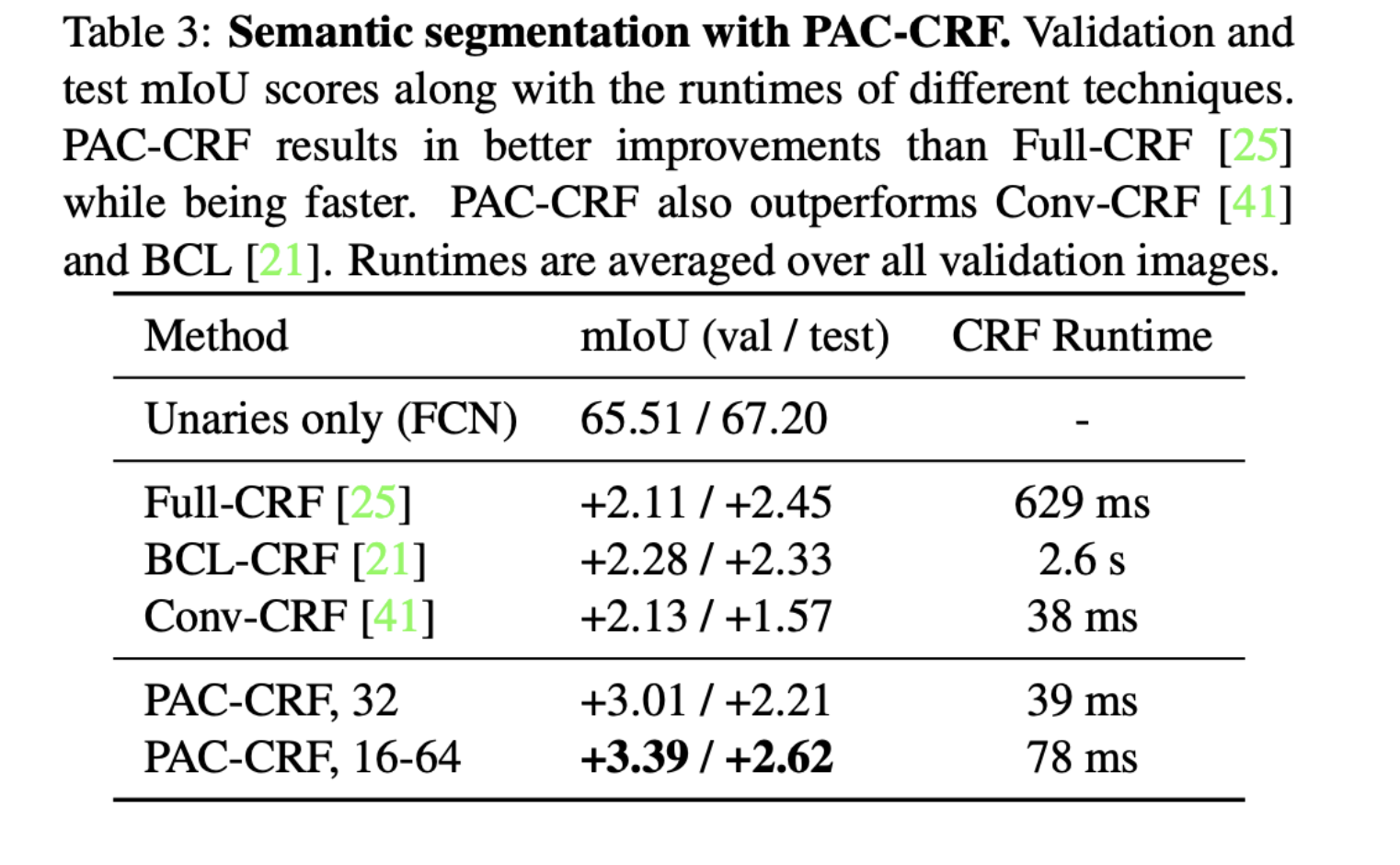
6. Layer hot-swapping with PAC
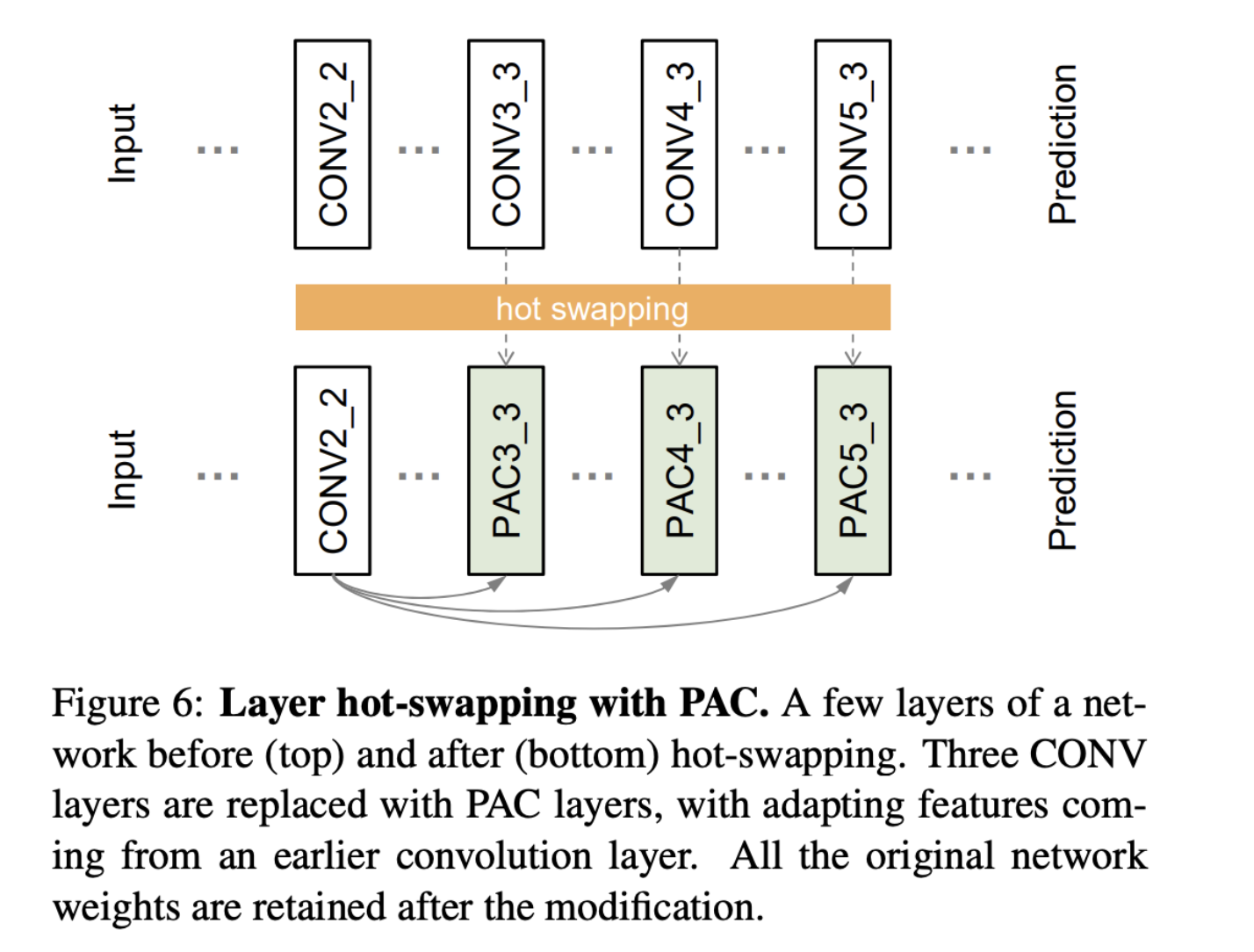
- 가장 적은 수정으로 기존 CNN을 업그레이드하기 위해 제시한 방법
- Layer hot-swapping
- fine-tuning에서 보통 새롭게 추가된 layer는 random initialized 된 상태
- PAC는 pre-trained weights를 유지한 채로 network의 convolution layer를 대체 가능
- FCN의 CONV2_2의 output을 guidance image로 설정하고 CONV3_3, CONV4_3, CONV5_3을 layer hot-swapping으로 PAC로 대체하여 학습
- 간단한 layer hot-swapping으로 더 좋은 성능을 내는데 성공

7. Conclusion
- guidance image의 information을 사용하여 학습하는 새로운 타입의 filtering operation, PAC를 제시
- 널리 쓰이는 필터까지 커버하는 뛰어난 generalization 성능
- joint upsampling, CRF inference, semantic segmentation 등에 적용 가능
- layer hot-swapping method로 간단하게 convolution layer를 대체하여 삽입 후 학습 가능
후기 & 정리
- Convolution 연산 자체를 Adaptive 하게 할 수 있도록 해주는 PAC를 제시
- NVIDIA 논문으로 NVIDIA에서 주로 사용
- Guidance image을 사용하여 만든 adapting kernel K 를 사용하여 기존 convolution의 문제인 spatially sharing, content-agnostic 문제를 해결
- layer hot-swapping으로 쉽게 pre-trained convolution layer를 대체할 수 있어 활용성이 높고 편리함
- Guidance image에서 얻은 정보를 사용하여 구성한 adapting kernel K 에 대한 추가적인 분석이 있었으면 좋았을 듯 함
Reference
[1] Hangsu et al. (2019). Pixel-Adaptive Convoltional Neural Networks, https://arxiv.org/abs/1904.05373
'AI > Deep Learning' 카테고리의 다른 글
| ArcFace: Additive Angular Margin Loss for Deep Face Recognition (0) | 2021.12.13 |
|---|---|
| You Only Look Once: Unified, Real-Time Object Detection (0) | 2021.11.30 |
| MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications (0) | 2021.11.06 |
| Adaptive Convolutional Kernels (0) | 2021.11.05 |
| Full Stack Deep Learning Lecture 5 ~ 7 (0) | 2021.10.30 |





