| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- animation retargeting
- ddpm
- CNN
- 모션매칭
- 딥러닝
- deep learning
- NLP
- 생성모델
- UE5
- Diffusion
- dl
- ue5.4
- 디퓨전모델
- BERT
- motion matching
- userwidget
- WBP
- Unreal Engine
- GAN
- Generative Model
- RNN
- WinAPI
- 언리얼엔진
- Stat110
- cv
- Font Generation
- 오블완
- Few-shot generation
- 폰트생성
- multimodal
- Today
- Total
Deeper Learning
Bayes' theorem 본문
농어와 연어를 분류하는 문제
- 생선의 길이를 기준으로 농어, 연어를 분류
길이를 x, 물고기의 종류를 w 라고 하자
물고기가 농어면 w=w1, 연어면 w=w2로 정의
Prior
사전확률인 Prior는 사전지식을 반영
연어가 농어보다 3배 많다면 P(w1)=0.25,P(w2)=0.75
전체 사건 확률의 합은 항상 1이 되어야 함
Posterior
모든 x에 대해 P(w1|x),P(w2|x) 값을 알면 두 값의 비교를 통해 쉽게 분류가 가능하다
즉, 길이 x가 주어졌을 때 두 클래스 w1,w2에 속할 확률을 알게되면 분류 문제를 해결한 것
이 확률 P(wi|x)를 Posterior라고 함
Likelihood
확률밀도 P(x|wi)는 물고기의 품종, 길이를 알고 있으면 얻을 수 있는 값으로 관찰을 통해 도출

Prior를 사용하지 않고 Likelihood 정보만 사용하여 x 가 12일 때, P(x=12|w2)>P(x=12|w1) 이므로 길이가 12일때 이를 연어라고 추정이 가능.
하지만 이는 P(w2|x=12) 와 다르게 prior 정보가 반영되지 않은 Likelihood를 통해 내린 결론으로 만약 P(w1)=0.999,P(w2)=0.001 로 대부분 농어가 잡히는 환경이라면 해당 추정의 정확도는 매우 낮을 것이다.
Prior를 고려하지 않고 Likelihood를 최대화 하는 방식을 ML(Maximum likelihood)이라고 하며 추가적인 regularization이 추가되지 않은 neural net의 경우 ML 방식으로 학습
Bayes Rule
조건부 확률 공식에 따라 아래 식을 유도할 수 있음
P(wi|x)=P(x|wi)P(wi)P(x)
w 의 모든 사건에 따라 식을 변형하면
P(wi|x)=P(x|wi)P(wi)P(x)=P(x|wi)P(wi)∑jP(x|wj)P(wj)
좌변은 Posterior, 우변의 분자는 Likelihood x Prior, 우변의 분모는 Evidence
P(w1)=2/3,P(w2)=1/3 일 때 Posterior 그래프.
Posterior를 최대로 하는 decision 방식을 MAP(Maximum a Posterior)라고 한다.
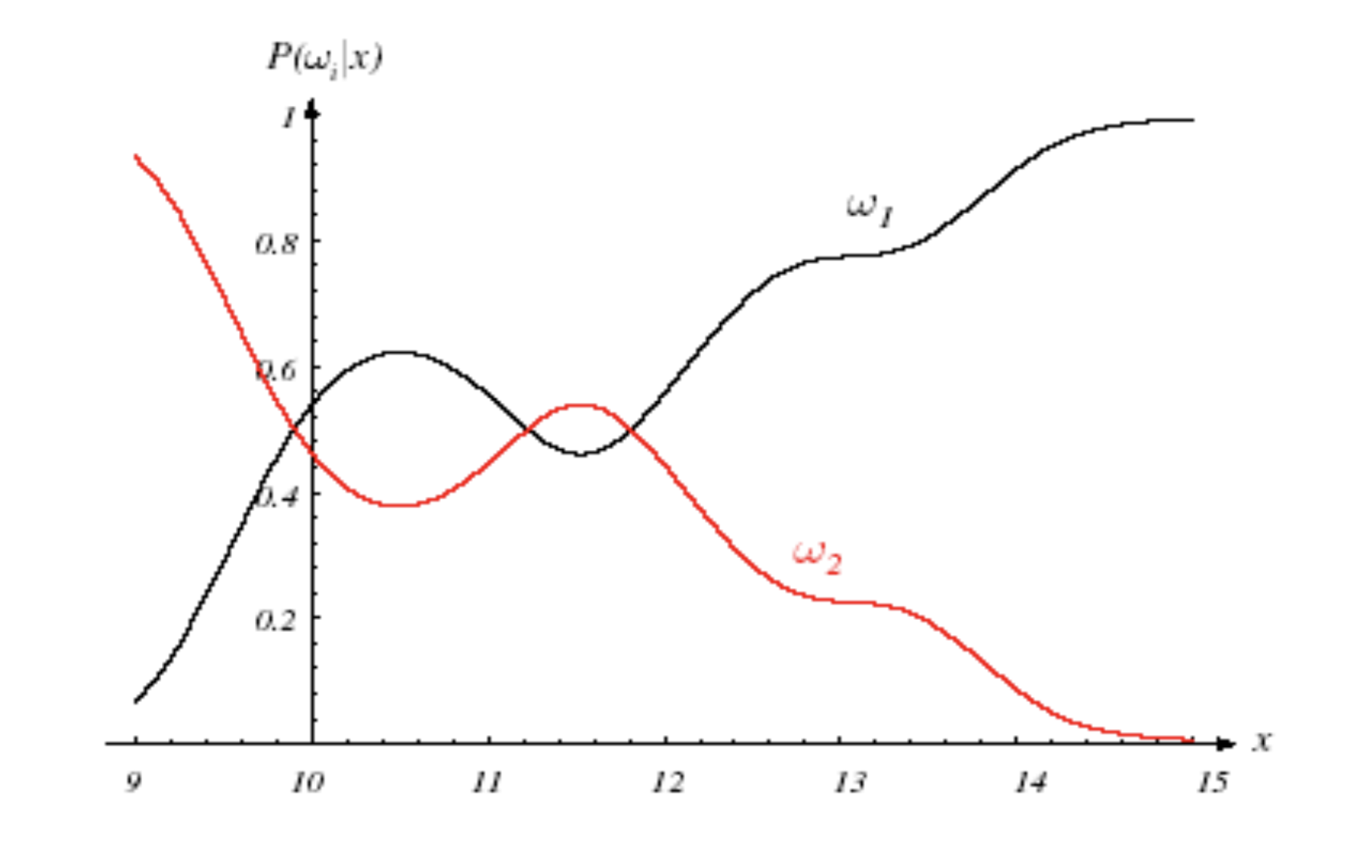
농어가 잡힐 확률이 높다는 Prior 정보가 반영되었기 때문에 길이가 12일 때 ML에서와 다르게 MAP에서는 농어로 예측.
ML은 prior가 uniform distribution인 MAP의 special case
Deep Learning에서의 MAP와 MLE에 대해서 다음에 기술 예정
Reference
[0] https://cse.buffalo.edu/~jcorso/t/CSE555/
'Statistics & Math' 카테고리의 다른 글
| Gram-Schmidt Process & QR Decomposition (0) | 2022.11.01 |
|---|---|
| [Statistics 110] Law of the unconscious statistician (LOTUS) (0) | 2022.05.21 |
| [Statistics 110] Universality of Uniform distribution (0) | 2022.05.21 |
| [Statistics 110] 확률변수와 확률분포 (0) | 2022.03.27 |
| Eigenvector & Eigenvalue (0) | 2021.07.20 |




