[Statistics 110] Law of the unconscious statistician (LOTUS)

LOTUS

law of the unconscious statistician (무의식적인 통계학자의 법칙, 이하 LOTUS)

통계학에서 확률변수 $X$의 함수 $g(X)$ 의 분포를 모르는 상황에서도 $g(X)$의 기댓값 $E(g(X))$를 계산할 수 있도록 해주는 theorem

---

Formula

1. discrete random variable X, f_X는 Probability mass function(pmf)

2. continuous random variable $X$, $f_X$는 probability density function(pdf)

---

Example

포아송 확률변수 $X$의 확률 분포의 기댓값, 분산을 구하는 문제, 우선 기댓값을 구해보면

매클로린 급수를 이용할 수 있도록 식을 유도

분산을 구하기 위해서 $Var(X) = E(X^2) - {E(X)}^2$에서 $E(X^2)$을 추가로 구하여야 하는데, LOTUS를 이용하여 이 값을 쉽게 계산할 수 있다.

 

기댓값을 계산할 때 구하였던 매클로린 급수 식에서 양변을 미분하고 $\lambda$값을 곱하는 과정을 2번 반복하여 얻은 수식을 사용하여 $E(X^2)$를 쉽게 구할 수 있다.

 

---

Proof

1. $X$가 이산확률 변수, $Y = g(X)$, $f_X(x) = pmf$ (단, $g$는 미분가능한 함수, $g^{-1}$는 monotonic)

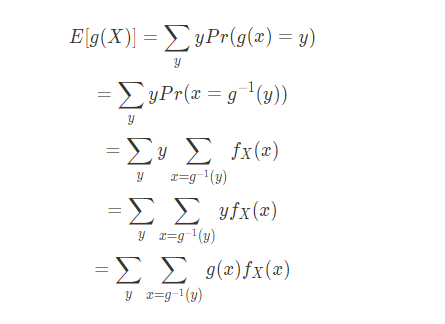
마지막 줄에서 시그마의 밑을 말로 풀면 모든 $y$에 대한 모든 $x(x=g^{-1}(y))$가 되는데 $g^{-1}$이 monotonic한 조건하에 이는 모든 $x$와 같기 때문에 식은 아래와 같다.

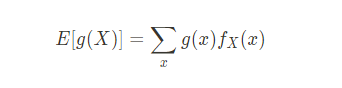
2. $X$가 연속확률 변수, $Y=g(X)$, $f_X(x)$ = pdf

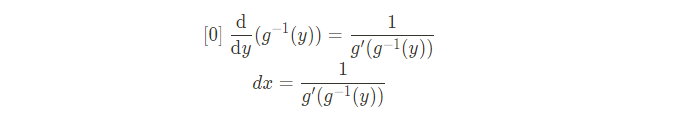
역함수를 미분하여 얻은 $dx$의 표현식을 $\int^{}_{X}g(x)f_X(x)dx$에 대입하면

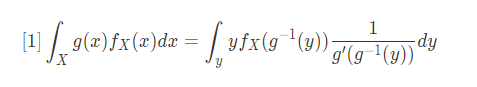
$Y$의 c.d.f 식을 활용

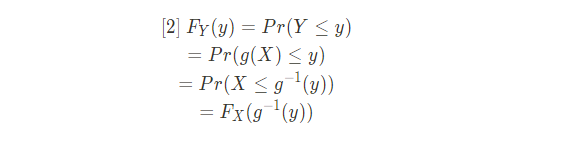
$Y$의 cumulative distribution function(cdf)를 미분하면 $Y$의 pdf를 얻을 수 있다.

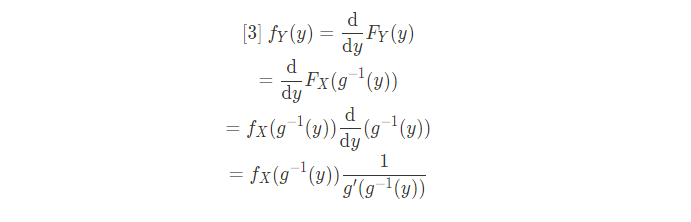
위 수식의 전개

• 앞서 정의한 등식 [2]를 사용하여 $F_Y(y)$를 $F_X(g^{-1}(y))$로 변환
• 합성함수의 미분 실행
• 앞서 정의한 등식 [0]을 사용하여 $\frac{d}{dy}(g^{-1}(y))$를 $\frac{1}{g'(g^{-1}(y))}$로 변환

앞서 정리한 등식 [1]에 [3]을 대입하여 마무리

---

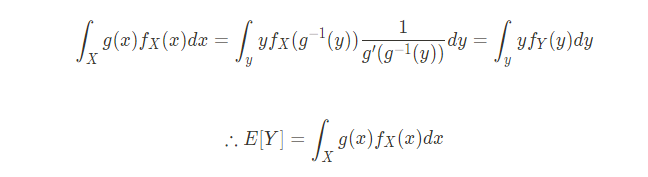
Reference

[0] Wikipedia: "Law of the unconscious statistician"

[1] https://statproofbook.github.io/P/mean-lotus.html