Gram-Schmidt Process & QR Decomposition

Gilbert Strang의 MIT 18.06SC Linear Algebra 완강 후 딥러닝 논문 스터디, 개인 학습 중 다시 마주한 선형 대수 개념 정리 목적

Gram-schmidt Process

linear independent column vectors를 직교화 해주는 방법론, orthogonal basis를 찾는 과정

 

Idea

 

선형독립인 두 벡터 $v_1, v_2$ 를 직교하는 두 벡터 $u_1, u_2$ 로 만들기 위해서는 우선 하나의 벡터 $v_1$ 을 $u_1$ 으로 두고 $v_2$ 를 $u_1$ 이 span하는 line에 정사영내린 $proj_{u_1}v_2$ 를 구하고 이를 $v_2$ 에서 빼주면 $u_1$ 과 직교하는 벡터 $u_2$ 를 얻을 수 있다.

 

Process

linear independent column vectors set $\{v_1,v_2\}$ 로 구성된 2x2 행렬 $V, v_i \in R^2$ 를 예시로 들겠다.

$$V = \{v_1 = \begin{bmatrix} 3\\ 1\end{bmatrix}, v_2 = \begin{bmatrix} 2\\ 2\end{bmatrix}\}$$

먼저 $v_1 = u_1$ 으로 설정하면

$$u_1 = \begin{bmatrix} 3\\ 1\end{bmatrix}$$

다음으로 $proj_{u_1}v_2$ 를 구하기 위해 쓰이는 벡터간 projection 식 유도 ( $\alpha_1$ 는 scalar, $\hat b$ 는 $b$ 와 같은 방향성을 가지는 unit vector)

$a$ 를 $b$ 에 정사영 내린 벡터 $a_1$ 은 scale(length)을 나타내는 scalar 값 $\alpha_1$ 과 direction을 나타내는 unit vector $\hat b$ 로 표현이 가능하다

 

$$[1] \space a_1 = \alpha_1 \hat b$$

 

cosine, dot product을 사용하여 $a_1$ 의 scale $\alpha_1$ 를 다음과 같이 표현가능하다

 

$$[2] \space\alpha_1 = \left \| a \right \|\cos \theta = a \cdot \hat b$$

 

[1] 식을 다시 써보면

 

$$a_1 = \alpha_1 \hat b = (a \cdot \hat b)\hat b$$

 

$b$ 의 unit vector $\hat b$ 는 $\frac{b}{\left \| b \right \|}$ 와 같기 때문에 이를 대입하면

 

$$(a \cdot \hat b)\hat b = \frac{a \cdot b} {\left \| b \right \|} \frac{b}{\left \| b \right \|} = \frac{a \cdot b}{\left \| b \right \|^2}b = \frac{a \cdot b}{b \cdot b}b$$

 

구한 vector projection 식을 활용해서 계산하면

 

$$proj_{u_1}v_2 = \frac{8}{10}v_2 = \frac{8}{10}\begin{bmatrix} 3\\ 1\end{bmatrix}$$

 

$u_1$ 이 span하는 space에 projection한 $proj_{u_1}v_2$ 를 $v_2$ 에서 빼면 가장 상단의 Figure에서 본 것 처럼 $u_1$ 에 직교하는 벡터 $u_2$ 를 얻을 수 있다

 

$$u_2 = v_2 - proj_{u_1}v_2 = \begin{bmatrix} 2\\ 2 \end{bmatrix}-\frac{8}{10}\begin{bmatrix} 3\\ 1\end{bmatrix}\begin{bmatrix} -2/5\\ 6/5\end{bmatrix}$$

 

구한 $u_1,u_2$ 를 크기가 1인 벡터로 normalize하면 orthonormal set $\{e_1,e_2\}$ 를 구할 수 있다

 

$$e_1 = \frac{1}{\sqrt{10}}\begin{bmatrix} 3\\ 1\end{bmatrix}, e_2 = \frac{1}{\sqrt {10}} \begin{bmatrix} -1\\ 3\end{bmatrix}$$

 

column vector가 3개 이상일 때의 식은 다음과 같다.

$u_3$ 는 $u_1, u_2$ 에 모두 직교하여야 하므로 $v_3$ 를 $u_1, u_2$ 에 projection 한 값을 빼주며 직교 벡터를 구한다.

 

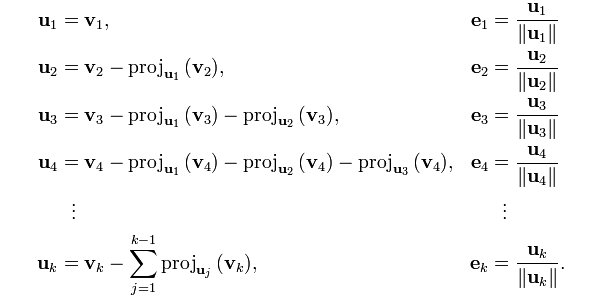
추가논의

• Gram-schmidt process로 얻은 정규화된 직교 벡터 set을 사용하면 다시 기존 벡터 set $V$ 를 재구성할 수 있다 (임의의 벡터가 아닌 $v_i$ 를 첫 orthogonal basis로 설정하고 프로세스를 시작했기 때문에 가능)
• linear dependent 벡터 set에서 위 과정을 진행한다면 최소 하나의 vector에서 $v_i = proj_{u_j}v_i$ 인 상황이 발생하기 때문에 $u_i = v_i - v_i$ 가 영벡터가 되는 문제가 존재
• 선형대수에서 orthonormal basis는 unique coefficients 측면에서 매우 중요한 의미를 가진다 (후에 많은 개념에서 활용)

---

QR Decomposition

 

Idea

위에서 언급한 것처럼 orthonormal basis를 활용하여 원본 벡터 set을 만들 수 있다 → 원복 벡터 set을 orthonormal columns을 가진 행렬과 upper triangle 행렬로 분해가 가능하다

 

Process

추가논의

• QR decomposition가 중요한 이유는 Gram-schmidt와 동일하게 직교성에 있다
• orthonormal matrix의 여러가지 성질은 선형대수에서 자주 활용됨
  • $QQ^T = I$
  • least square에서 용이한 계산
  • etc

 

Reference

• https://en.wikipedia.org/wiki/Gram–Schmidt_process
• https://en.wikipedia.org/wiki/Vector_projection
• https://en.wikipedia.org/wiki/QR_decomposition
• https://darkpgmr.tistory.com/165