Diffusion Model 수식 정리

prerequisite: Diffusion Model에 대한 기초적인 이해

Diffusion Model

$T$ = 전체 Timesteps 수

$x_T$ = forward process를 $T$ 번 적용한 마지막 Timestep $T$ 에서의 이미지

$x_0$ = 원본 이미지

 

Forward Process

$$ q(x_t|x_{t-1}) = N(x_t, \sqrt{1-\beta_t}x_{t-1}, \beta_tI) $$

$\beta$ 는 noise(variance)의 강도를 조절하는 parameter로 DDPM 논문에서는 0.0001 ~ 0.02의 값을 사용

$\beta$ 가 선형적으로 timesteps에 따라(DDPM에서는 linear noise scheduler 사용) 0.0001에서 0.02까지 증가하면 $\sqrt{1-\beta_t}$ 는 1에서 0.989.. 까지 감소

$x_{250}$ 을 구하려면 위 one-step forward process를 250번 거쳐야 하는데 이는 병렬적으로 처리가 불가능한 프로세스라 시간이 오래 걸리는 문제가 있음.

한 번에 $x_0$ 에서 임의의 timestep $t$ 의 $x_t$ 를 구할 수 있는 방법이 있는데 이를 설명하기 위해 notation을 추가로 정의해보자.

$$ \alpha_t = 1-\beta_t $$

$$ \bar{\alpha_t} = \prod_{s=1}^{t}\alpha_s, \space q(x_t|x_{t-1}) = N(x_t, \sqrt{\alpha_t}x_{t-1}, (1-\alpha_t)I) $$

 

Reverse Process

$$ p_{\theta}(x_{t-1}|x) $$

forward process와 반대로 denoise 하는 process, parameter set $\theta$ 를 가지는 모델을 사용

 

Training Objective 수식 Ver.1

Marginalize

$$ p(x) = \int p(x,z)dz $$

Expectation

$$ E_x(f(x)) = \int xf(x)dx $$

Chain rule

$$ p(x) = \frac{p(x,z)}{p(z|x)} $$

$$ p(x,z) = p(z|x)p(x) $$

 

MLE objective $\log p(x)$ 에서 시작

(34) $x_{1:T}$ 와 joint distribution을 Marginalize

$$ \log p(x) = \log \int p(x_0, x_{1:T})dx_{1:T} = \log \int p(x_{0:T})dx_{1:T} $$

(35) $1=\frac{q(x_{1:T})}{q(x_{1:T})}$ 를 곱해준다

(36) Expectation의 정의를 사용하여 정리

(37) Jensen’s inequality로 만든 부등식

(38) Chain rule 활용

T = 2 라고 하면

$$ q(x_{1:2}|x_0) = q(x_1,x_2|x_0) = q(x_2|x_0,x_1)q(x_1|x_0) $$

이전 state에만 영향을 받는 Markov property에 의하여

$$ q(x_2|x_0,x_1)q(x_1|x_0) = q(x_2|x_1)q(x_1|x_0) $$

일반화하면

$$ q(x_{1:T}|x_0) = \prod_{t=1}^Tq(x_t|x_{t-1}) $$

reverse process 부분도 마찬가지로 Chain rule을 활용하면

$$ p(x_{0:T}) = p(x_T)p(x_{0:T-1}|x_T) = p(x_T)\prod_{t=1}^Tp_\theta(x_{t-1}|x_t) $$

(39) timestep T, 1에 해당하는 수식을 분리

(40) t의 범위를 조정

(41) log 성질 활용

(42) log 성질 활용

(43) 셋째 항에서 Expectation 시그마 안으로 이동

(44) Expectation의 term을 각 항에서 사용하는 변수로 한정

(45) KL-divergence의 정의와, joint distribution에서 Expectation의 marginalize 성질을 활용하여 전개

$$ KL(p||q) = \int_x p(x)\log(\frac {p(x)}{q(x)})dx = E_{x \sim p}[\log(\frac{p(x)}{q(x)})] $$

$$ E_{q(x_{T-1},x_T|x_0)}[\log \frac{p(x_T)}{q(x_T|x_{T-1})}] = -E_{q(x_{T-1},x_T|x_0)}[\log \frac{q(x_T|x_{T-1})}{p(x_T)}] $$

$$ = -E_{q(x_{T-1}|x_0)q(x_T|x_{T-1})}[\log \frac{q(x_T|x_{T-1})}{p(x_T)}] =-E_{q(x_{T-1}|x_0)}\int_xq(x_T|x_{T-1})[\log \frac{q(x_T|x_{T-1})}{p(x_T)}] dx = -E_{q(x_{T-1}|x_0)}[D_{KL}(q(x_T|x_{T-1})||p(x_T))] $$

셋 째항도 마찬가지로 정리하면

 

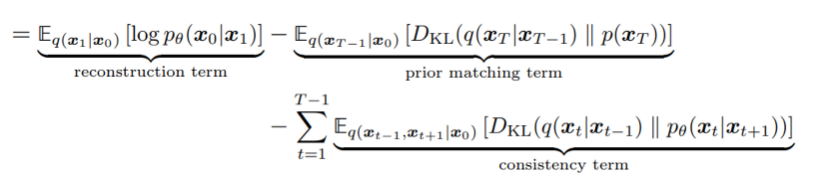
첫째항은 첫 forward process를 거친 이미지가 주어지고 원본 데이터의 log probability를 예측하는 reconstruction term으로 해석할 수 있으며 해당 term은 VAE에서도 등장

 

둘째항은 마지막 timestep의 $x_T$ 의 분포가 Gaussian prior와 일치하는지 계산하는 prior matching term으로 학습가능한 parameter가 없기 때문에 optimization이 이루어지지 않는다. (전체 timestep이 충분히 클 경우 마지막 forward process를 거친 데이터는 Gaussian을 따른다는 가정도 있음)

 

셋째항은 consistency term으로 $x_t$ 에서 분포가 consistent 하도록 하는 역할을 하는데 모든 timestep에서 denoising step의 분포를 대상 데이터의 한 step 전의 noising step과 맞추도록 KL-divergence를 사용한다.

 

Ground-truth Denoise step & Approximate Denoise step

 

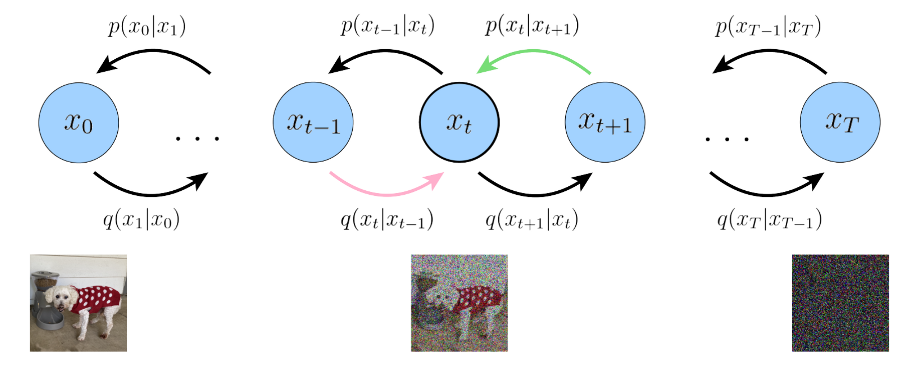
위에서 전개한 Training objective의 consistency term는 매 timestep에서 $q(x_t|x_{t-1})$ 와 $p(x_t|x_{t+1})$ 을 matching하는 방식으로 VDM(variational diffusion model)을 최적화 할 수 있다.

 

최종 Training objective의 식은 모두 기댓값을 사용하는데 이는 Monte Carlo 추정을 통해 근사할 수 있다. 여기에서 문제가 하나 있는데, 우리가 도출한 ELBO는 모든 timestep에서 두 random variables $x_{t-1},x_{t+1}$ 에 대한 기댓값을 사용하는 것이다. (consistency term에서)

 

timestep마다 하나의 random variable을 사용하는 것보다 2개의 random variables을 사용하면 Monte Carlo 추정에서 variance가 더 커지는 문제가 생긴다.

 

Training Objective 수식 Ver.2

 

timestep마다 하나의 random variable에 대한 기댓값만 사용하도록 수식을 다시 정리할 필요가 있다.

바로 이전 단계의 state에만 영향을 받는 Markov Property에 따라 $x_0$ 를 추가 조건으로 주어도 식은 동일하다.

$$ q(x_t|x_{t-1}) = q(x_t|x_{t-1},x_0) $$

$$ q(x_t|x_{t-1},x_0) = \frac{q(x_{t-1}|x_t,x_0)q(x_t|x_0)}{q(x_{t-1}|x_0)} $$

새로 정리한 forward process의 수식을 통해 다시 Training objective 식을 전개해보자 (37) ELBO 부분부터 이어서 시작하면

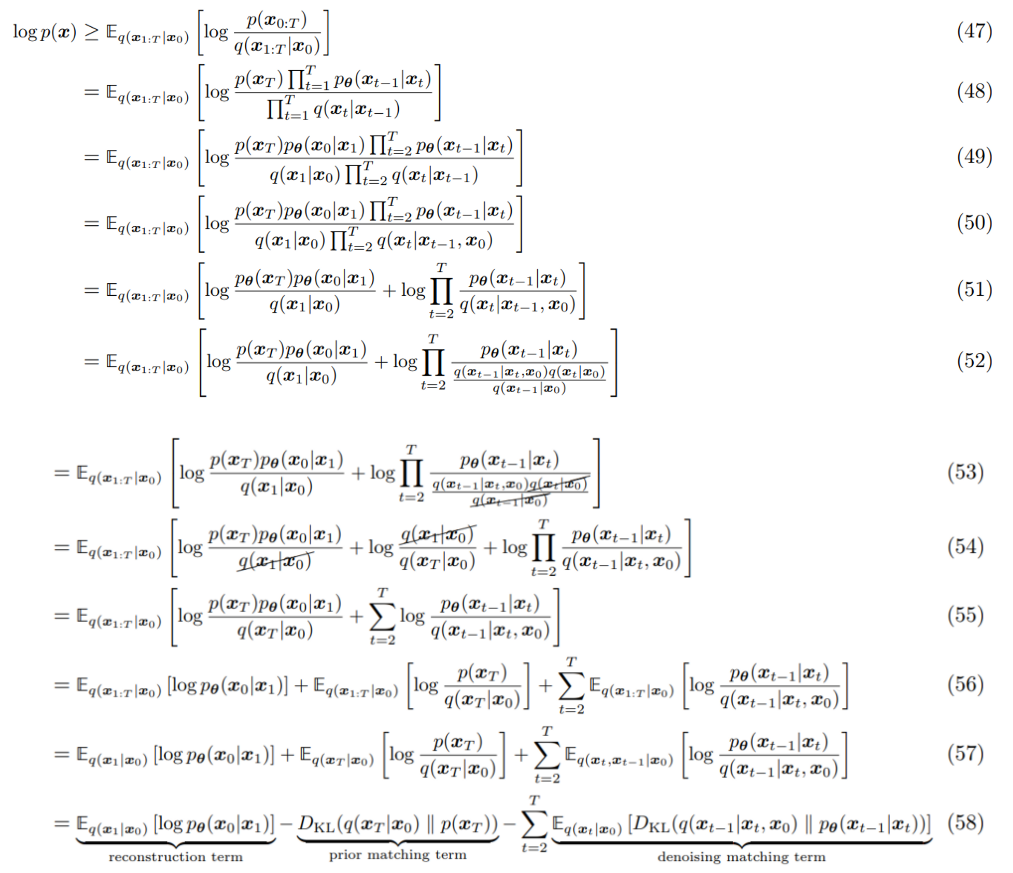
(48) (38)과 동일

(49) t=1에 해당하는 식을 밖으로 빼서 따로 표기

(50) Markov property로 인해 $x_0$ 을 condition에 추가하여도 동일한 식

(51) log 성질에 따라 항 분리

(52) 새로 정리한 forward process 수식 $q(x_t|x_{t-1},x_0) = \frac{q(x_{t-1}|x_t,x_0)q(x_t|x_0)}{q(x_{t-1}|x_0)}$ 대입

(53)

$$ \prod_{t=2}^T \frac{q(x_{t-1}|x_t,x_0)q(x_t|x_0)}{q(x_{t-1}|x_0)} = \frac{q(x_{1}|x_2,x_0)q(x_2|x_0)}{q(x_{1}|x_0)}\frac{q(x_{2}|x_3,x_0)q(x_3|x_0)}{q(x_{2}|x_0)} ... \frac{q(x_{T-1}|x_T,x_0)q(x_T|x_0)}{q(x_{T-1}|x_0)} $$

소거되는 항 $q(x_2|x_0),q(x_3|x_0)...$ 을 모두 소거하면 아래와 같다.

$$ \prod_{t=2}^T \frac{q(x_{t-1}|x_t,x_0)q(x_t|x_0)}{q(x_{t-1}|x_0)} = \frac{q(x_T|x_0)}{q(x_1|x_0)}\prod_{t=2}^T q(x_{t-1}|x_t,x_0) $$

이를 활용해서 식을 전개

(54) 소거

(55) log 성질에 따라 항 합침

(56) log 성질에 따라 항 분리

(57) Expectation의 대상이 되는 변수만 표기

(58) (45)번 전개방식과 동일하게 Expectation과 KL divergence의 관계를 활용

 

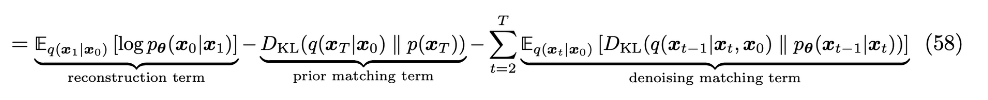
첫째항, 둘째항은 이전 전개와 동일하게 해석할 수 있다.

 

셋 째항은 denoising matching term 으로 tractable ground-truth denoising transition step인 $q(x_{t-1}|x_t,x_0)$ 에 모델이 예측한 denoising step $p_{\theta}(x_{t-1}|x_t)$ 가 가까워지도록 하는 역할을 한다. $q(x_{t-1}|x_t,x_0)$ 는 noisy image $x_t$ 를 완벽히 denoise한 이미지 $x_0$ 정보를 가지고 denoise를 하기 때문에 ground-truth signal의 역할을 한다.

 

 

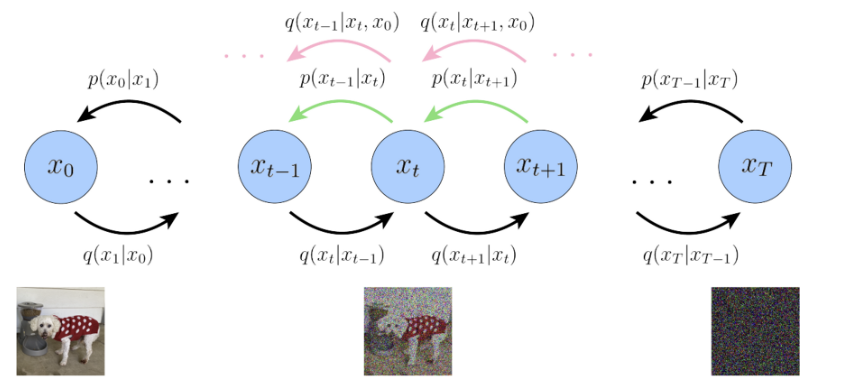
처음 전개한 식과 다르게 이제 timestep마다 하나의 random variable에 대한 Expectation을 계산한다. (처음과 다르게 초록, 분홍색 화살표의 condition이 동일하여 방향이 같음)

 

Ground-truth Denoising Step 수식 정리

 

이렇게 새로 구한 Training objective에서 아직 해결되지 않은 문제가 있다. denoising matching term의 ground-truth denoising transition step $q(x_{t-1}|x_t,x_0)$ 를 어떻게 나타낼지인데, 우선 Bayes Rule을 사용해보면 아래와 같다.

$$ q(x_{t-1}|x_t,x_0) = \frac{q(x_t|x_{t-1},x_0)q(x_{t-1}|x_0)}{q(x_t|x_0)} $$

forward process는 위에서 정의한 것을 사용하면

$$ q(x_t|x_{t-1},x_0)=q(x_t|x_{t-1}) = N(x_t;\sqrt{\alpha_t}x_{t-1},(1-\alpha_t)I) $$

남은 term인 $q(x_t|x_0),q(x_{t-1}|x_0)$ 는 아래의 reparameterization trick을 사용해 정리한다.

$$ x \sim N(x;\mu,\sigma^2) $$

$$ x = \mu + \sigma \epsilon, \space \epsilon \sim N(\epsilon, 0, I) $$

이를 활용해서 $x_t\sim q(x_t|x_{t-1}), x_{t-1}\sim q(x_{t-1}|x_{t-2})$ 를 다시 써보면

$$ x_t\sim q(x_t|x_{t-1}) = N(x_t;\sqrt{\alpha_t}x_{t-1},(1-\alpha_t)I)\\ \space x_t = \sqrt\alpha_tx_{t-1}+\sqrt{1-\alpha_t}\epsilon, \space \epsilon \sim N(\epsilon;0,I) \space (59) $$

$$ x_{t-1}\sim q(x_{t-1}|x_{t-2}) = N(x_{t-1};\sqrt{\alpha_{t-1}}x_{t-2},(1-\alpha_{t-1})I)\\ x_{t-1} = \sqrt\alpha_{t-1}x_{t-2}+\sqrt{1-\alpha_{t-1}}\epsilon, \space \epsilon \sim N(\epsilon;0,I) \space (60) $$

$\{\epsilon_t^*,\epsilon_t\}_{t=0}^T \sim i.i.d.\space N(\epsilon ;0,I)$ 와 같이 2T개의 random noise variables를 정의하고 이제 이를 모두 활용하여 $x_t \sim q(x_t|x_0)$ 을 전개해보자

 

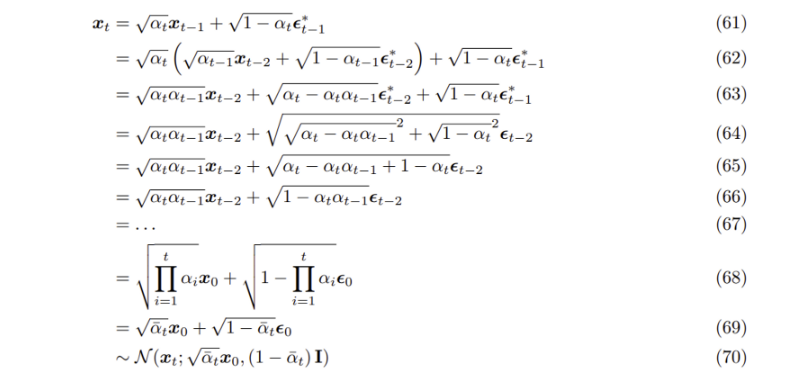
(61) 앞서 reparameterization trick을 사용해 구한 (59)식 사용

(62) 앞서 reparameterization trick을 사용해 구한 (60)식 사용

(63) $\sqrt{\alpha_t}$ 를 곱해주는 분배법칙

(64)

$\sqrt{\alpha_t-\alpha_t\alpha_{t-1}}\epsilon_{t-2}^*$ 는 reparameterization trick을 사용하면 반대로 평균이 0이고 분산이 $\alpha_t - \alpha_t\alpha_{t-1}$ 인 가우시안 분포 $N(0, (\alpha_t-\alpha_t\alpha_{t-1})I)$ 의 sample로 생각할 수 있다.

$\sqrt{1-\alpha_t}\epsilon_{t-1}^*$ 도 마찬가지로 $N(0, (1-\alpha)I)$ 분포의 sample로 여길 수 있으며 두 가우시안 분포의 합은 각 가우시안 분포의 평균의 합이 평균이고, 분산의 합이 분산인 새로운 가우시안 분포가 되기 때문에(하단 수식 참고) (64)식으로 정리가 가능하다.

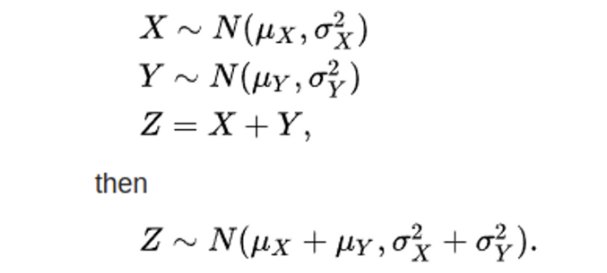
(65) 제곱근과 제곱 풀기

(66) $\alpha_t$ 정리

(67, 68) (61)에서 $x_{t-1},\epsilon_{t-1}^*$ 를 정리하면 (66)처럼 되는데 이를 timestep t에서 0까지 반복하고 이를 정리한 식

(69) $\alpha$ 의 timestep에 따른 누적곱을 새롭게 정의

$$ \bar \alpha =\prod_{i=1}^t\alpha_i $$

(70) reparameterization trick에 의해 해당 random variable이 따르는 분포를 가우시안 분포로 표현

이제 $x_0$ 에서 한 번에 $x_t$ 로의 forward process를 식으로 아래와 같이 나타낼 수 있게 되었다

$$ q(x_{t}|x_0) = N(x_t;\sqrt{\bar\alpha_t}x_0, (1-\bar\alpha_t)I) $$

 

이제 정리가 필요한 term을 모두 정리하였으니 딥러닝 모델의 denoise process가 근사하기를 바라는 ground-truth denoising transition step $q(x_{t-1}|x_t,x_0)$ 수식을 simplify 해보자.

 

(71) $x_t,x_{t-1}$ 에 Bayes Rule 적용

(72) 앞서 정리한 수식 대입

(73) 비례관계 기호와 함께 Gaussian 분포의 P.D.F 식 사용, $\alpha$ 로 구성된 상수항은 비례기호 하에 생략 가능

(74) 공통으로 항들에 포함된 1/2을 괄호 밖으로

(75) 제곱을 풀고 $x_0,x_t$ 로만 구성된 항들을 따로 정리

$$ \exp\{-\frac{1}{2}[\frac{(x_t^2-2x_t\sqrt\alpha_tx_{t-1}+\alpha_tx_{t-1}^2)}{1-\alpha_t}+\frac{x_{t-1}^2-2\sqrt{\bar{\alpha}}{t-1}x{t-1}x_0+\bar{\alpha}{t-1}x_0^2}{1-\bar\alpha{t-1}}-\frac{x_t^2-2x_t\sqrt{\bar{\alpha_t}}x_0+\bar\alpha_tx_0^2}{1-\bar{\alpha}_t}]\} $$

$$ = \exp\{-\frac{1}{2}[\frac{x_t^2}{1-\alpha_t}+\frac{-2x_t\sqrt\alpha_tx_{t-1}+\alpha_tx_{t-1}^2}{1-\alpha_t}+\frac{x_{t-1}^2-2\sqrt{\bar{\alpha}}{t-1}x{t-1}x_0}{1-\bar\alpha_{t-1}}+\frac{\bar{\alpha}{t-1}x_0^2}{1-\bar\alpha{t-1}}-\frac{x_t^2-2x_t\sqrt{\bar{\alpha_t}}x_0+\bar\alpha_tx_0^2}{1-\bar{\alpha}_t}]\} $$

$$ = \exp\{-\frac{1}{2}[\frac{(-2x_t\sqrt\alpha_tx_{t-1}+\alpha_tx_{t-1}^2)}{1-\alpha_t}+\frac{(x_{t-1}^2-2\sqrt{\bar{\alpha}}{t-1}x{t-1}x_0)}{1-\bar\alpha_{t-1}}+\frac{x_t^2}{1-\alpha_t}+\frac{\bar{\alpha}{t-1}x_0^2}{1-\bar\alpha{t-1}}-\frac{x_t^2-2x_t\sqrt{\bar{\alpha_t}}x_0+\bar\alpha_tx_0^2}{1-\bar{\alpha}_t}]\} $$

$$ = \exp\{-\frac{1}{2}[\frac{(-2x_t\sqrt\alpha_tx_{t-1}+\alpha_tx_{t-1}^2)}{1-\alpha_t}+\frac{(x_{t-1}^2-2\sqrt{\bar{\alpha}}{t-1}x{t-1}x_0)}{1-\bar\alpha_{t-1}}+C(x_t,x_0)]\} $$

(76) $C(x_t,x_0)$ 을 비례기호를 사용하여 제거, 분자에서 항을 따로 표현

(77) $x_{t-1}^2, x_{t-1}$ 을 기준으로 식을 묶어 표현

(78) 첫째항에서 덧셈 부분을 계산

(79, 80) 첫째항의 분자 부분 계산, $\alpha_t$ 가 지워짐

(81) $\frac{1-\bar{\alpha_t}}{(1-\alpha_t)(1-\bar{\alpha_{t-1}})}$ 로 식을 묶어 표현

(82) $x_{t-1}$ 가 포함된 항의 분자, 분모에 $(1-\alpha_t)(1-\bar{\alpha}_{t-1})$ 를 곱해주어 식을 정리

(83) $(1-\alpha_t)(1-\bar{\alpha}{t-1})$ 를 $x{t-1}$ 가 포함된 항에서 분배법칙을 이용하여 정리, 앞의 coefficient 부분에서는 $1-\bar\alpha_t$ 로 분자, 분모를 나누어줌

(84) Gaussian distribution의 p.d.f를 정리해보면

$$ N(x_{t-1},\mu,\sigma^2) = \frac{1}{\sqrt{2\pi}\sigma} \exp\{-\frac{1}{2}{(\frac{x_{t-1}-\mu}{\sigma})}^2\} \\ \propto \exp \{{-\frac{1}{2}(\frac{x_{t-1}-\mu} {\sigma})}^2\} = \exp \{{-\frac{1}{2}(\frac{1}{\sigma^2})(x_{t-1}-\mu})^2\} = \exp \{{-\frac{1}{2}(\frac{1}{\sigma^2})(x_{t-1}^2-2x_{t-1}\mu +\mu^2})\} $$

 

정리한 식을 (83)의 식과 비교해보면

$$ \mu = \frac{\sqrt{\alpha_t}(1-\bar{\alpha}{t-1})x_t+\sqrt{\bar{\alpha}{t-1}}(1-\alpha_t)x_0}{1-\bar{\alpha_t}} \\ \sigma^2 = \frac{(1-\alpha_t)(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t} $$

 

$\mu, \sigma$ 가 위와 같은 Gaussian 분포의 p.d.f와 비슷한 것을 볼 수 있다.

 

$\mu^2$ 부분이 빠져있는데, $\mu$ 가 $x_t,x_0$ 으로 구성된 항이기 때문에 (75)에서 $C(x_t,x_0)$ 을 상수항으로 여기며 비례기호를 사용하여 식에서 배제한 것 처럼 비례기호를 사용하여 $\mu^2$ 이 추가되었다고 가정하면 Gaussian distribution 꼴로 식을 만들 수 있다.

 

이제 Ground truth denoising step은 Gaussian 분포로 모델링 되었으며 식은 아래와 같다.

$$ q(x_{t-1}|x_t,x_0) \propto N(x_{t-1};\frac{\sqrt{\alpha_t}(1-\bar{\alpha}{t-1})x_t+\sqrt{\bar{\alpha}{t-1}}(1-\alpha_t)x_0}{1-\bar{\alpha_t}},\frac{(1-\alpha_t)(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}) $$

 

Denoising Matching Term 수식 정리

 

$$ q(x_{t-1}|x_t,x_0) \propto N(x_{t-1};\frac{\sqrt{\alpha_t}(1-\bar{\alpha}{t-1})x_t+\sqrt{\bar{\alpha}{t-1}}(1-\alpha_t)x_0}{1-\bar{\alpha_t}},\frac{(1-\alpha_t)(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}) $$

위 식에서 variance는 timestep에 따라 고정된 상수인 $\alpha$ term으로만 구성되어 있기 때문에 모델이 예측하는 denoising step $p_{\theta}(x_{t-1}|x_t)$ 의 Variance는 Ground-truth denoising step의 variance를 그대로 사용하면 되기 때문에 $\mu_\theta(x_t,t)$ 를 parameterize하는 것만 남았다.

Denoising matching term을 다시보면 Ground-truth denoising step에 모델이 예측한 denoising step을 근사시키기 위해 KL Divergence를 사용하는데 둘다 Gaussian 분포로 모델링하였기 때문에 KL Divergence 식이 아래처럼 간단해진다.

$$ D_{KL}(N(x;\mu_x,\Sigma_x)||N(y;\mu_y,\Sigma_y)) = \frac12[\log\frac{|\Sigma_y|}{|\Sigma_x|} -d+tr(\Sigma_y^{-1}\Sigma_x)+(\mu_y-\mu_x)^T\Sigma_y^{-1}(\mu_y-\mu_x)] $$

 

GT(Ground truth) reverse process $q$ 와 모델이 구한 reverse process $p$ 는 둘 다 Gaussian 으로 모델링 되었으며 variance는 $\alpha$ 로 구성한 상수로 동일하게 세팅되어 있는 상태에서 Denoising Matching Term의 수식을 정리해보자.

 

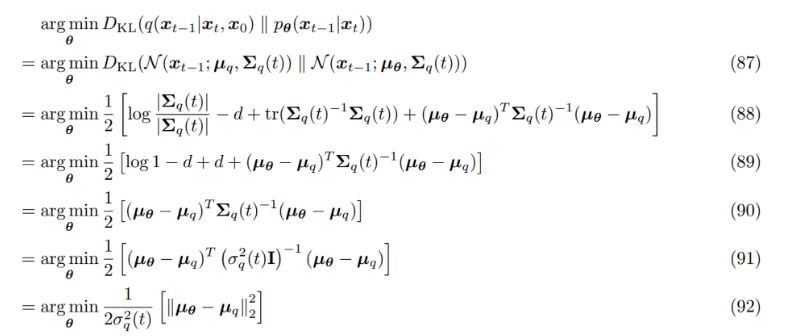
(87) 은 앞에서 구한 GT denoising step, 모델이 근사하는 denoising step을 Gaussian 형태로 표현한 것, variance는 $\alpha$ 로 구성되어 있어 따로 추정하지 않고 GT denoising step의 variance를 그대로 사용

(88) 두 다변량 Gaussian 분포의 Kullback–Leibler divergence 식을 사용

(89) 앞서 forward process를 정의할 때 Diagonal covariance matrix로 정의하였기 때문에 inverse matrix는 element에 역수를 취한것과 같고 원본 covariance matrix와 그 inverse matrix를 곱하면 Identity matrix가 되며 Trace를 구하면 dimension $d$ 와 같다.

(90) log1=0, -d+d=0

(91) Diagonal covariance matrix 이기 때문에 Identity matrix와 상수부로 분리

(92) 역행렬은 각 element의 역수를 취한것과 동일 하고 variance가 각 변량에서 동일하기 때문에 상수로 표현가능하여 대괄호 밖으로 뺄 수 있음

 

벡터를 Transpose하고 원본 벡터와 곱하는 것은 벡터의 원소들의 제곱의 합인데 Frobenius norm은 벡터에서 원소들의 제곱의 합에 square root를 씌운것이기 때문에 argmin 하에 등호 사용가능

 

Denoising matching term에서 우리가 원하는 것은 이제 GT(이하 Ground truth, forward process의 수식으로 구한 denoising step) mean과 모델이 예측한 mean 값의 L2 norm이 가장 작아지는 model parameter set $\theta$ 를 구하는 것이 되었다.

 

앞서 (84) 에서 구한 GT denoising step의 mean의 수식은 아래와 같다.

$$ \mu_q(x_t,x_0,t) = \frac{\sqrt{\alpha_t}(1-\bar{\alpha}{t-1})x_t+\sqrt{\bar{\alpha}{t-1}}(1-\alpha_t)x_0}{1-\bar{\alpha_t}} $$

$t,x_0,x_t$ 값과 상수 $\alpha_{t}$ 로 식이 구성되어 있는데 모델을 통해 근사하려는 $\mu_\theta(x,t)$ 는 Noise가 없는 원본 데이터 $x_0$ 의 정보가 없다는 차이점이 있다.

$x_t$ 의 정보는 동일하게 가지고 있기 때문에 이를 대입하면

$$ \mu_\theta(x_t,t) = \frac{\sqrt{\alpha_t}(1-\bar{\alpha}{t-1})x_t+\sqrt{\bar{\alpha}{t-1}}(1-\alpha_t)\hat x_\theta(x_t,t)}{1-\bar{\alpha_t}} $$

 

$x_0$ 은 모델의 추정이 필요한 값으로 모델은 $x_t,t$ 를 사용하여 원본 이미지 $x_0$ 를 예측해야 한다.

새롭게 얻은 GT denoising step의 $\mu_q$, predicted denoising step의 $\mu_\theta$ 식을 대입하여 (92)에 이어서 식을 정리해보자.

 

(96) (92)식에서 새로 얻은 $\mu_q,\mu_\theta$ 식 대입

(97) 두 항에서 동일한 $x_t$ term 빼서 제거

(98) $\frac{\sqrt{\bar\alpha_{t-1}}(1-\alpha_t)}{1-\bar\alpha_t}$ 로 식을 묶음

(99) 상수부분을 Frobenius norm 밖으로 빼냄

(100) 임의의 timestep 2~T에서의 수식

 

Variational Diffusion Model(VDM)의 최적화는 neural network가 임의의 timestep의 noisy image에서 원본 GT image를 추정하면서 이루어진다.

 

Learning Diffusion Noise Parameters

 

앞서 forward process에서 $\alpha$ 는 1에서 최소값과 최대값을 정하고 timestep에 따라 일정하게 증가하는 $\beta$ 를 빼서 계산한 timestep에 따라 fix된 상수로 정의하였는데 이를 neural net이 학습하도록 하는 방식도 있다.

 

단순하게 새로운 neural net을 사용하여 각 time step의 $\alpha_t$ 를 예측하게 할 수 있는데 문제점은 $\alpha$ 의 cumulative product인 $\bar \alpha_t$ 를 매번 새롭게 계산해야하는 computational cost가 발생한다는 것이다.

 

위에서 전개한 수식을 활용하면 더 효율적인 방식을 찾을 수 있다.

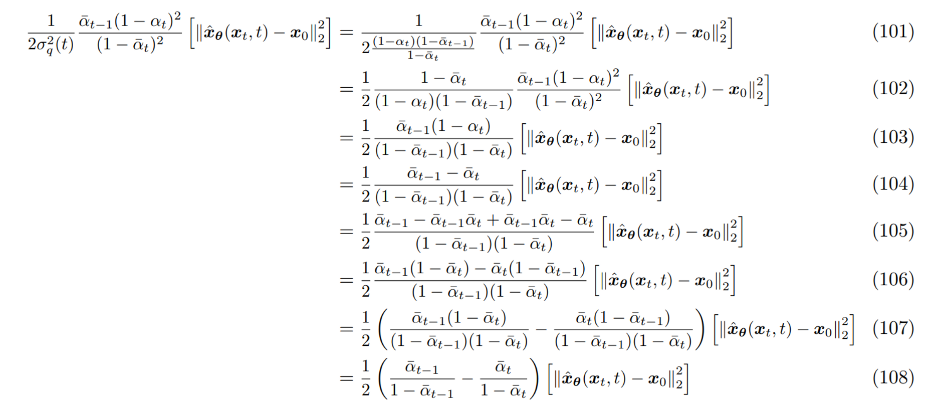
(101) (99) 수식에서 시작, 앞서 구한 GT denoising step 수식에서 분산 부분 수식을 대입

$$ q(x_{t-1}|x_t,x_0) \propto N(x_{t-1};\frac{\sqrt{\alpha_t}(1-\bar{\alpha}{t-1})x_t+\sqrt{\bar{\alpha}{t-1}}(1-\alpha_t)x_0}{1-\bar{\alpha_t}},\frac{(1-\alpha_t)(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}) $$

(102) $1-\bar{\alpha_t}$ 값을 분자, 분모에 곱해주어 식 저일

(103) 분자, 분모에서 동일한 식 소거

(104) $\bar{\alpha_t} = \alpha_t \times \bar{\alpha}_{t-1}$ 활용

(105) timestep에 따라 항을 나누기 위한 준비로 $\bar{\alpha}_{t-1}\bar\alpha_t$ 를 추가

(106) $\bar{\alpha}_{t-1},\bar\alpha_t$ 로 분자의 항 묶음

(107) 두 항으로 식 나누기

(108) 분자, 분모 동일식 소거하여 timestep에 따른 항 분리 완료

 

Signal-to-noise ratio(SNR)는 noise 대비 signal의 level로 여러 형태로 정의할 수 있는데 아래 형태를 사용하겠다. https://en.wikipedia.org/wiki/Signal-to-noise_ratio#Definition

$$ SNR=\frac{\mu^2} {\sigma^2} $$

 

이전에 정의한 $q(x_t|x_0)$ 에 SNR 식을 적용해보면

$$ q(x_t|x_0) = N(x_t;\sqrt{\bar\alpha_t}x_0,(1-\bar\alpha_t)I) \\ \\SNR(t) = \frac{\bar\alpha_t}{1-\bar\alpha_t} $$

SNR 식을 (108) 수식에 사용해보자

 

SNR

 

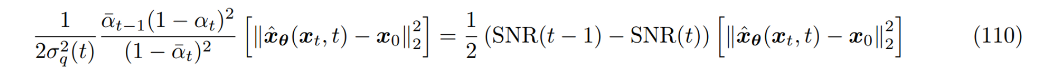
마지막 timestep T에 도달하였을 때, standard Gaussian이 되기 위해서는 SNR은 t가 커질 수록 점차 작아져야하기 때문에 SNR을 parameters $\eta$ 를 가지는 단조 증가 neural net $\omega_\eta(t)$ 로 모델링하자

 

$$ SNR(t) = \exp(-\omega_\eta(t)) $$

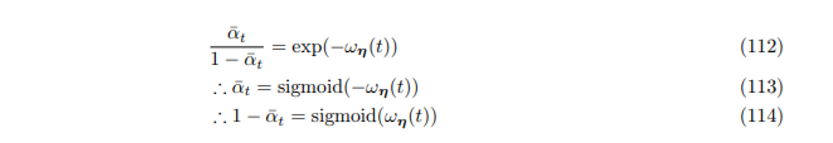
(112) 위에서 정한 SNR 식 대입

(113) Sigmoid 식 꼴로 식 변형

$$ a = \bar\alpha, b = \omega_\eta(t)\\ \frac {a}{1-a} = \exp(-b) \\a = \exp(-b)(1-a)\\a = \exp(-b) - a \exp(-b) \\ a+a \exp(-b) = \exp(-b) \\ a(1+ \exp(-b)) = \exp(-b)\\ a = \frac{ \exp(-b)}{1+ \exp(-b)} = \frac{1}{1+\exp(b)} = \frac{1}{1+ \exp(-(-b))} \\ sigmoid(z) = \frac{1}{1+\exp(-z)} \\ a = sigmoid(-b)\\ \bar\alpha_t = sigmoid(-\omega_\eta(t))\\ 1-a = 1-\frac{1}{1+\exp(b)}= \frac{\exp(b)}{ 1+\exp(b)}= \frac{1}{1+\exp(-b)} = sigmoid(b) \\ 1-\bar\alpha_t = sigmoid(\omega_\eta(t)) $$

 

Neural Net의 output에 sigmoid를 씌운 값이 $1-\bar\alpha_t$ 를 추정하도록 하면 $\alpha_t$ 를 직접적으로 추정하고 그 누적곱을 매번 계산하지 않아도 된다.

(실제 코드에서는 UNet model의 output의 dimension을 2배로 설정하고 반으로 나누어 epsilon(or original image) prediction, sigma prediction 으로 사용)

 

Epsilon Prediction

 

VDM은 neural net이 $t,x_t$ 가 주어진 상황에서 원본 이미지 $x_0$ 를 추정하는 방식으로 학습되는 것을 앞서 확인하였다.

 

원본 데이터 $x_0$를 다른 term으로 나타낼 수 있는데 여러 forward step을 한 번에 정의한 식에 reparameterization trick을 사용하면 $x_0$ 가 $x_t,\epsilon_0$ 에 대한 식으로 정리된다.

 

$$ q(x_{t}|x_0) = N(x_t;\sqrt{\bar\alpha_t}x_0, (1-\bar\alpha_t)I) \\ x_t = \sqrt{\bar\alpha_t}x_0 + \sqrt{1-{\bar\alpha_t}}\epsilon_0\\x_0 = \frac{x_t - \sqrt{1-{\bar\alpha_t}}\epsilon_0}{\sqrt{\bar\alpha_t}} (115) $$

 

(84)에서 구한 ground-truth denoising step의 mean의 수식과 approximate denoising step의 수식을 보면 모델에게 정보가 없는 $x_0$ 만 모델의 예측값으로 대체되는데 바로 위(115)에서 얻은 식을 사용하여 $x_0$ 를 $x_t,\epsilon_0$ 에 대한 식으로 바꾸면 모델은 $\epsilon_0$ 를 예측해야하는 상황이 된다. (epsilon prediction)

 

$$ \mu_q(x_t,x_0,t) = \frac{\sqrt{\alpha_t}(1-\bar{\alpha}{t-1})x_t+\sqrt{\bar{\alpha}{t-1}}(1-\alpha_t)x_0}{1-\bar{\alpha_t}} $$

$$ \mu_\theta(x_t,t) = \frac{\sqrt{\alpha_t}(1-\bar{\alpha}{t-1})x_t+\sqrt{\bar{\alpha}{t-1}}(1-\alpha_t)\hat x_\theta(x_t,t)}{1-\bar{\alpha_t}} $$

(117) (115)에서 얻은 식을 대입하여 $x_0$ 를 $x_t,\epsilon_0$ 에 대한 식으로 변경

(118) $\bar\alpha_t$ 의 누적곱 성질을 활용하여 정리

$$ \sqrt{\bar\alpha_{t-1}} = \alpha_{t-1}\alpha_{t-2}...\alpha_0 \\ \sqrt{\bar\alpha_{t}} = \alpha_t\alpha_{t-1}...\alpha_0\\\frac{\sqrt{\bar\alpha_{t-1}}}{\sqrt{\bar\alpha_{t}}} = \frac{\alpha_{t-1}\alpha_{t-2}...\alpha_0 }{\alpha_t\alpha_{t-1}...\alpha_0} = \frac{1}{\alpha_t} $$

(119,120) $x_t,\epsilon_0$ 으로 식을 정리하기 위함

(121) $x_t$ 로 묶은 식의 첫 항에서는 분자, 분모에 $\sqrt{\alpha_t}$ 를 곱해주어 통분, $\epsilon_0$ 로 묶은 식에는 분자, 분모에 $\sqrt{1-\bar\alpha_t}$ 를 곱해주어 정리

(122,123,124) $x_t$ 의 계수부분 식 정리

 

새로 얻은 GT denoising step의 mean값을 근사하기 위해서 모델은 이제 $\epsilon_0$ 을 추정해야하며 그에따른 approximate denosing step의 mean의 식은 아래와 같다.

 

 

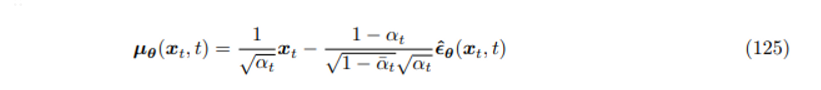
epsilon prediction 세팅으로 다시 denoising matching term의 수식을 전개해보자

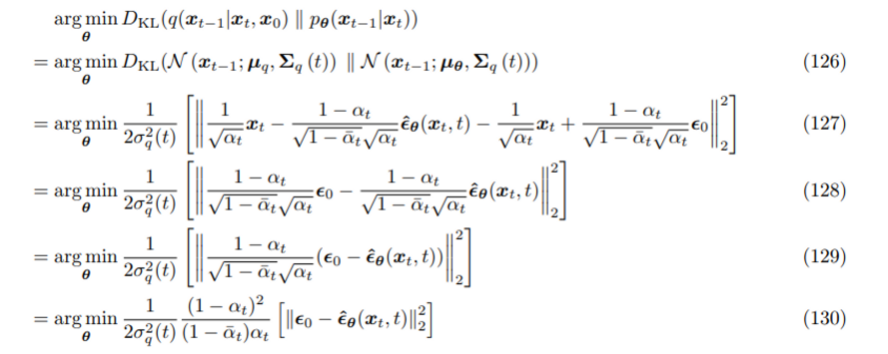
(127) (124)(125)에서 새로 얻은 $\mu_q,\mu_\theta$ 식 대입

(128) 두 항에서 동일한 $x_t$ term 빼서 제거

(129) $\frac{1-\alpha_t}{\sqrt{1-\bar\alpha_t}\sqrt{\alpha_t}}$ 로 식을 묶음

(130) 상수부분을 Frobenius norm 밖으로 빼냄

모델은 $x_t,t$ 가 주어진 상황에서 Standard Gaussian 분포를 따르는 $\epsilon_0 \sim N(\epsilon;0,I)$을 예측해야 한다.

 

VDM에서 원본 이미지 $x_0$ 을 예측하는 것은 $x_0$ 를 임의의 timestep t의 $x_t$ 로 만드는데 사용하는 noise $\epsilon$ 을 예측하는 것과 동일하다.

 

후기 & 정리

지금까지 아래 항목에 대해 다루었다.

1. forward process
2. reverse process
3. ELBO를 활용한 MLE Training objective 정리
4. 하나의 random variable이 condition이 되도록 다시 MLE Training objective 정리
5. Denoising matching term 정리
6. Noise parameter (Sigma, Variance) 학습 설정
7. Epsilon prediction 설정

여러 Diffusion 코드 베이스를 빠르게 파악하거나 다른 Diffusion 논문의 수식을 이해하고 구현하는데 도움이 될 것 같아 line by line으로 전반적인 Diffusion 모델의 수식을 정리해보았다.

 

log variance training, previous mean prediction, epsilon prediction, x0 prediction, learning sigma, simple loss 등과 같이 여러 개인 구현 Diffusion repo에서 통일되지 않은 용어로 세팅들을 설명하고 있는데 수식과 코드를 대조하면서 보면 더욱 쉽고 빠르게 코드를 이해할 수 있음.

 

주로 “Understanding Diffusion Models: A Unified Perspective” 논문을 참고하였는데 VAE와 HVAE 수식 전개, Score-based generative model, Classifier-free-guidance 같은 개념도 자세하게 설명되어있어 개인적으로 추천한다.

 

Reference

[0] https://minibatchai.com/diffusion/generative-models/text2image/2022/06/17/Diffusion.html

[1] https://vinesmsuic.github.io/paper-ddpm/#Parametrized-Reverse-Denoising-Diffusion-Process

[2] Calvin Lui. (2022). “Understanding Diffusion Models: A Unified Perspective”. https://arxiv.org/abs/2208.11970

Understanding Diffusion Models: A Unified Perspective