| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Diffusion
- ue5.4
- NLP
- 모션매칭
- deep learning
- 디퓨전모델
- WinAPI
- 오블완
- Generative Model
- animation retargeting
- cv
- 딥러닝
- Few-shot generation
- 생성모델
- dl
- CNN
- multimodal
- 언리얼엔진
- UE5
- GAN
- Stat110
- 폰트생성
- Unreal Engine
- userwidget
- BERT
- ddpm
- motion matching
- WBP
- RNN
- Font Generation
- Today
- Total
Deeper Learning
Improved-DDPM: Improved Denoising Diffusion Probabilistic Models 본문
Improved-DDPM: Improved Denoising Diffusion Probabilistic Models
Dlaiml 2023. 4. 19. 21:40Alex Nichol, Prafulla Dhariwal (2021.02) [openAI]
Abstract
- DDPM이 간단한 변경으로 높은 log-likelihoods 달성할 수 있다는 것을 보임
- reverse diffusion 과정의 분산을 학습하면 더 적은 forward process로 큰 퀄리티 차이 없이 sampling이 가능하다는 것을 발견
- GAN과 DDPM이 얼마나 타겟 분포를 커버하는지 비교하기 위해 precision, recall 사용
- 연산량, model capacity에 따라 샘플 퀄리티와 likelihood가 부드럽게 scaling 되는 것을 확인
- https://github.com/openai/improved-diffusion
GitHub - openai/improved-diffusion: Release for Improved Denoising Diffusion Probabilistic Models
Release for Improved Denoising Diffusion Probabilistic Models - GitHub - openai/improved-diffusion: Release for Improved Denoising Diffusion Probabilistic Models
github.com
1. Introduction
DDPM은 고품질의 이미지, 오디오 생성에 성공하였지만 autoregressive model, VAEs와 같은 다른 log-likelihood 기반 모델과 비슷한 성능을 내는 것은 보이지 못하였다. DDPM 논문에서 LSUN, CIFAR-10에서 놀라운 생성 결과를 보였으나 ImageNet과 같은 high-diversity 데이터셋으로의 scale 결과는 아직 밝혀지지 않았다.
본 논문에서는 DDPM이 ImageNet과 같은 high-diversity 데이터셋에서도 다른 likelihood 기반 모델과 비슷한 log-likelihoods를 달성하는 것을 보여준다. Improved-DDPM은 variational lower-bound(VLB)를 최적화하기 위해 간단한 reparameterization을 사용하여 reverse process의 분산을 학습하고 VLB와 DDPM의 simplified objective를 결합한 hybrid learning objective를 사용한다.
log-likelihood를 직접적으로 최적화 하는 것보다 hybrid objective를 최적화하였을 때 더 좋은 log-likelihood를 기록하였는데 이는 log-likelihood 자체를 최적화할 때 생기는 많은 gradient noise가 문제인 것으로 가설을 세우고 이를 개선하였다.
학습된 분산을 사용하면 샘플 퀄리티 감소는 거의 없으며 적은 step으로 샘플링이 가능한 것을 발견하였음. DDPM은 좋은 퀄리티의 샘플을 생성하기 위해 수백 steps이 필요하나 improved-DDPM은 50 forward passes로도 좋은 퀄리티의 샘플을 생성. 빠른 샘플링 method인 DDIM과 실험에서 비교.
likelihood가 좋은 metric이지만 GAN과 분포 coverage 측면에서 비교를 위해 precision, recall metric을 사용, diffusion 모델은 비슷한 FID에서 훨씬 높은 recall을 달성하여 타겟 분포의 많은 부분을 cover하고 있다는 것을 밝힘. DDPM에서 한 것과 같이 scalability를 측정, model size와 training compute를 증가시킬수록 성능이 예측가능하게 개선되는 추세를 확인하였음
2. Denoising Diffusion Probabilistic Models
(improved-DDPM과 DDPM의 차이점만 간략하게 소개)

VLB loss는 위 식과 같으며 L0 을 제외하고는 두 분포의 KL divergence로 이루어져 있다.
이미지 데이터에서 L0 은 각 채널이 256 구간으로 나뉘고 (0,1,…,255) 알맞은 구간에 값이 위치할 확률을 가우시안 분포의 CDF를 활용해서 구한다.
diffusion 모델에서 μθ(xt,t) 를 parameterize 하는 방식은 다양한데, μθ 를 바로 추정하거나 x0,ϵ 을 추정하는 방식도 있다.
DDPM 논문에서는 ϵ prediction을 택했으며 Lvlb 를 직접 최적화하는 것보다 아래 simple loss를 사용하는 것이 더 좋은 성능을 보였다고 한다.

3. Improved the Log-likelihood
DDPM은 높은 FID, IS를 기록하였지만 높은 log-likelihood를 기록하는데 실패하였다. log-likelihood는 생성 모델이 데이터 분포의 mode를 학습하도록 하는 역할을 한다고 알려져 있으며 log-likelihood가 조금만 개선되어도 샘플 퀄리티와 학습된 feature representation이 크게 좋아진다는 연구 결과가 존재한다.
따라서 DDPM이 왜 높은 log-likelihood를 달성하지 못하는가에 대한 분석 또한 매우 중요한데, 이번 장에서는 DDPM의 여러 요소를 변경하며 log-likelihood를 측정하고 변경 사항을 잘 조합하였을 때, DDPM도 다른 likelihood 기반 생성모델처럼 높은 log-likelihood를 달성할 수 있음을 보이려 한다.
모델과 데이터셋은 고정(ImageNet 64x64, CIFAR-10)하고 실험을 진행하였다.
DDPM의 세팅을 따르면 σ2t=βt,T=1000, 3.99 (bits/dim)의 log-likelihood를 얻을 수 있었으며, T=4000 의 세팅은 3.77 log-likelihood를 기록하였다. (200K training iterations 기준)
3.1. Learning Σθ(xt,t).
DDPM에서 저자는 Σθ(xt,t) 를 σ2tI 로 학습되지 않는 값인 σt 를 사용하였고 σ2t 를 βt 으로 고정하면 ˜βt 로 고정한 것과 비슷한 샘플 퀄리티를 보였다고 말했다.
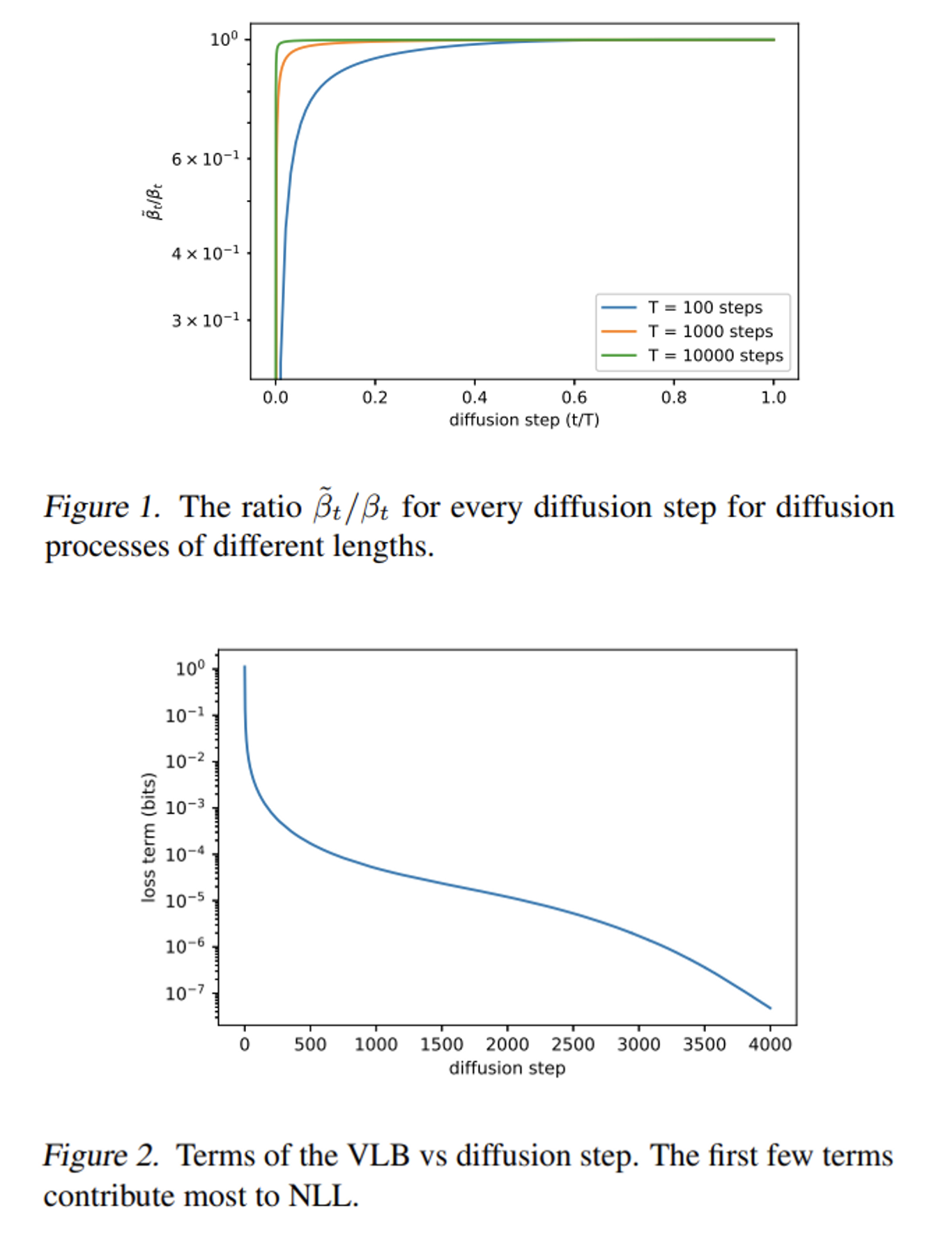
이는 위 [Figure 1]으로 설명이 가능한데, diffusion step T가 커질수록 분산이 샘플에 미치는 영향이 작아짐을 볼 수 있다.
σt 를 고정한 것은 위 그림으로 납득이 되지만 log-likelihood 측면에서는 [Figure 2]를 보면 초기 몇 스텝이 vlb에 크게 기여하기 때문에 Σθ 를 학습하면 log-likelihood를 개선할 수 있다고 저자는 주장한다.
하지만 모델이 바로 Σθ 를 학습하기에는 유효한 variance의 범위가 매우 작아 쉽지 않다. 이를 해결하기 위해 모델의 output을 β,˜β 의 interpolation 정도를 조절해 주는 vector v 로 설정하였다.

Lsimple 은 분산을 고려하지 않기 때문에 최종 loss인 hybrid objective를 아래와 같이 정하였다.
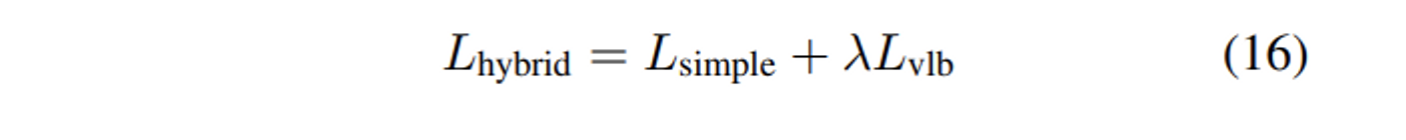
실험을 통해 λ 가 0.001일 때 vlb loss가 simple loss를 overwhelming하지 않는다는 것을 찾았고 vlb의 μ 에서는 stop gradient를 사용하여 simple loss가 μ 에 영향을 끼치는 메인 loss, vlb loss가 분산을 담당하도록 유도하였다.
3.2. Improving the Noise Schedule
DDPM의 linear noise schedule이 high resolution 이미지에서는 잘 작동하나 64, 32 resolution에서는 최적 세팅이 아님을 확인하였다.

[Figure 3]을 보면 후반부의 forward process는 이미지가 noise에 너무 가까워진 상태로 진행되며 이는 샘플 퀄리티에 큰 영향을 끼치지 않는다. [Figure 4]를 보면 reverse diffusion process의 일부를 skip해도 linear schedule의 경우 FID가 비슷한 것을 확인할 수 있다.
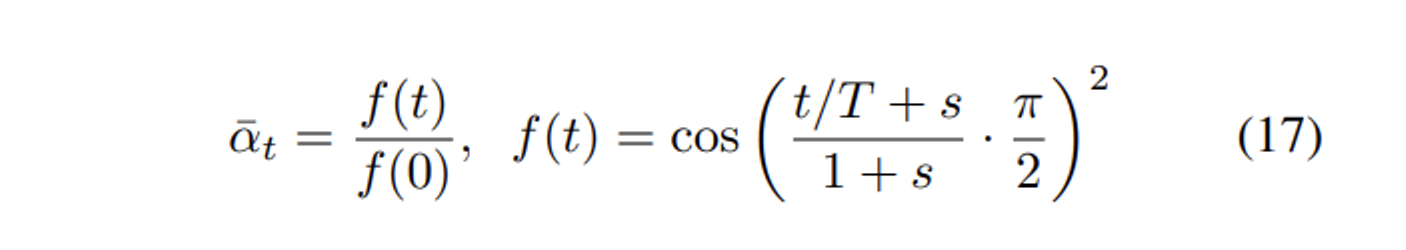
이를 개선하기 위해 저자는 위 수식의 cosine schedule을 제시하였다.
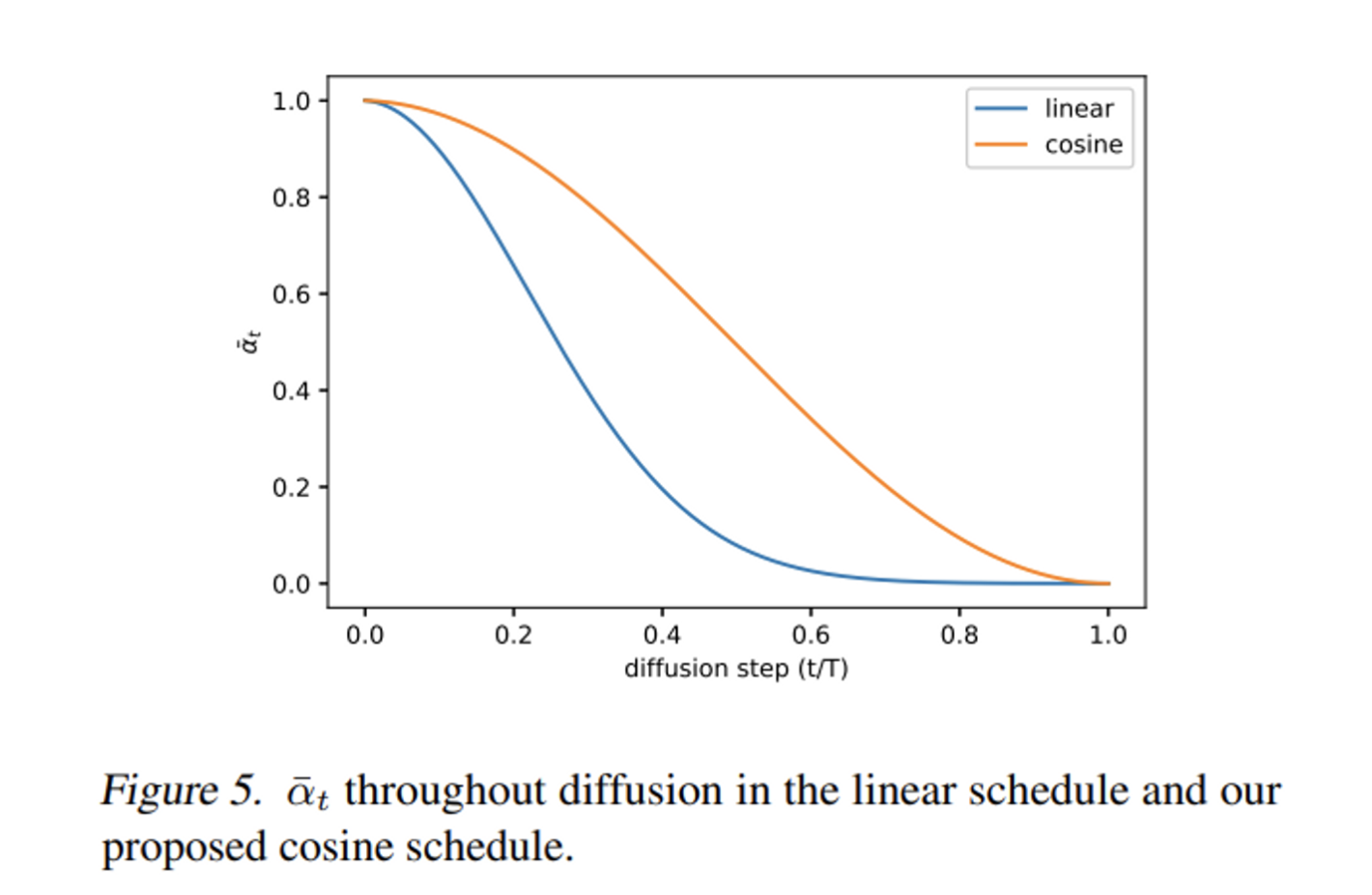
cosine schedule의 ˉαt 를 보면 linear schedule과 다르게 0으로 빠르게 감소하지 않고 중간 지점에서 linear한 감소 추세를 보인다.
βt=1−ˉαtˉαt−1 로 작은 offset s를 넣어 βt 가 t=0 근처에서 너무 작아지지 않도록 하였다. s는 √β0 이 pixel bin size인 1/127.5보다 조금 작아지도록 s=0.008로 설정하였다.
f(t) 를 보면 cosine의 square를 사용하였는데 원하는 shape(Figure 5)를 얻기 위해서 임의로 선택한 함수로 다른 함수의 사용을 추가 연구로 제시하였다.
3.3. Reducing Gradient Noise
hybrid loss가 아닌 vlb loss로 모델을 최적화하면 가장 좋은 log-likelihood를 달성할 것이라고 기대하였지만 실제로는 vlb loss를 사용한 최적화가 분산이 큰 ImageNet 데이터셋에서는 쉽지 않다는 것을 실험을 통해 발견하였음.
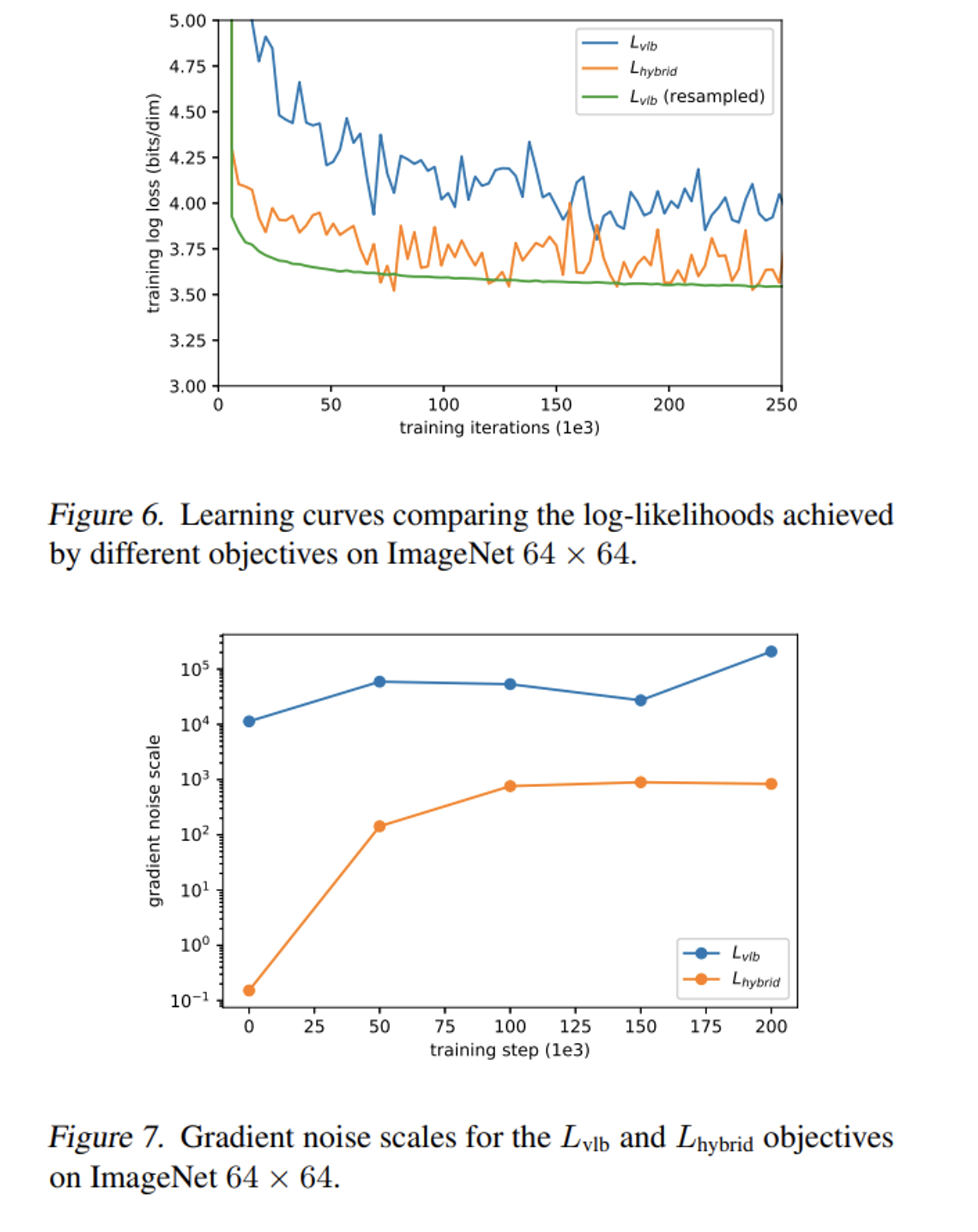
[Figure 6]는 각각 vlb, hybrid, resampled vlb loss로 학습한 모델의 loss graph인데 vlb loss보다 hybrid loss를 사용하였을 때 더 좋은 log-likelihood를 기록한 것을 볼 수 있다.
vlb loss의 gradient가 더 noisy 할 것이라고 저자는 가설을 세웠고 gradient noise scale을 뽑아본 결과 실제로 그러하였다. [Figure 7]
[Figure 2]를 보면 학습하면서 sampling한 timestep에 따라 log-likelihood에 미치는 영향이 매우 다른데 uniform하게 t를 샘플링하는 방식이 불필요한 noise를 발생시킨다고 생각하였고 이를 해결하기 위해 importance sampling을 사용하였다.

학습 초기에는 각 timestep의 Loss에 대한 정보가 없기 때문에 모든 timestep에서 10개의 sample을 뽑기 전에는 uniform 샘플링을 사용한다.
[Figure 6]을 보면 importance sampling을 사용한 vlb의 경우 loss의 noise가 매우 작아진 것을 볼 수 있다. 하지만 hybrid loss에 importance sampling을 적용할 때는 큰 효과가 없었다.
3.4. Results and Ablations
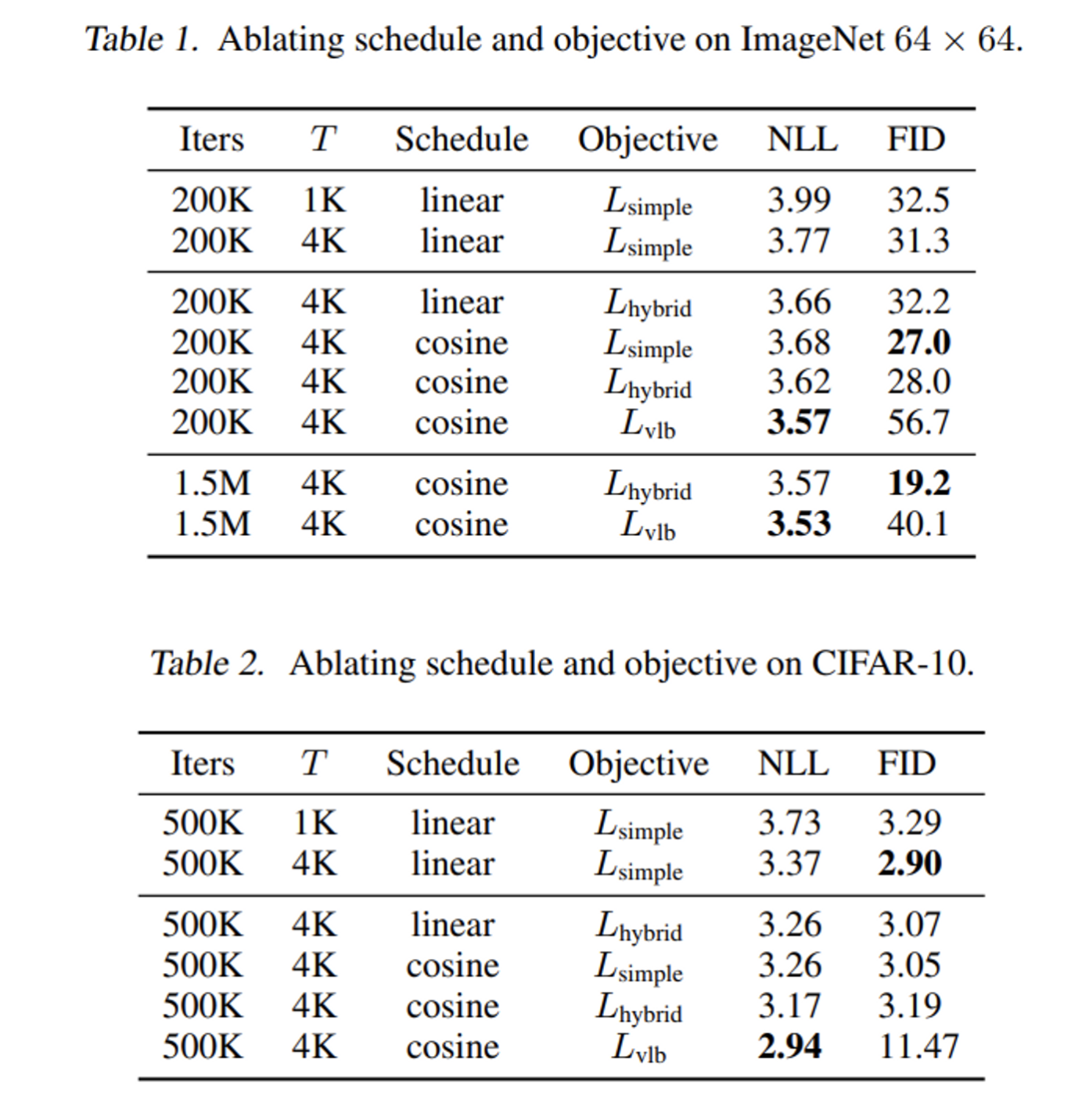
vlb, hybrid loss는 learned sigma 세팅으로 학습하였으며 vlb loss는 앞서 소개한 importance sampling scheme을 사용하였다.
cosine schedule, hybrid loss를 사용하면 비슷한 FID를 유지하면서 log-likelihood를 개선할 수 있었으며 vlb loss를 사용하면 FID를 희생하지만 log-likelihood는 더욱 좋아지는 것을 확인하였다. 저자는 hybrid loss가 샘플 퀄리티를 유지하면서 log-likelihood를 개선하기 때문에 hybrid loss를 일반적으로 선호한다고 언급하였다.

다른 log-likelihood 기반 모델과 비교하여도 Improved DDPM은 괜찮은 성능을 보임
4. Improving Sampling Speed
실험은 모두 4000 diffusion steps을 사용하였기 때문에 샘플링에는 수 분이 걸린다. 이번 섹션에서는 샘플링 단계에서 step을 줄였을 때 샘플 퀄리티를 확인하려 한다.
hybrid loss로 학습된 모델에서 학습 때 사용한 step 보다 훨씬 적은 step을 사용하여 샘플링해도 고품질의 결과를 생성할 수 있다는 것을 실험하였다.
학습 시 1~T의 diffusion steps을 사용하였으면 보통 1~T step을 사용하여 샘플링하지만 이를 subsequence인 S 를 사용하여 샘플링할 수도 있다.

위와 같이 새로 sampling variance가 정의되고 Σθ(xSt,St) 또한 βSt,˜βSt 사이에 위치해야 하기 때문에 더 짧은 diffusion process를 따라 rescale되며 새로운 diffusion process가 정의된다. (분산을 interpolation weight로 정의하였기 때문에 beta가 변경되어도 그대로 적용가능)

[Figure 8]은 25, 50, 100, 200, 400, 1000, 4000 sampling steps에서의 결과를 나타낸 것이며 mid-training, fully trained는 각각 CIFAR-10에서 200K, 500K iterations, ImageNet에서 500K, 1500K iterations을 의미한다.
sigma가 고정된 Lsimple 모델은 샘플링 timestep이 줄어듬에 따라 성능에 큰 타격을 받았지만 sigma를 학습하며 Lhybrid 를 사용하는 모델은 좋은 샘플 퀄리티를 유지하였다.
학습이 완료된 모델에서 제시한 세팅(learned sigmas, hybrid loss)는 학습에 사용한 4000 steps의 1/40인 100 step에서도 좋은 성능을 보였다.
DDIM과 비교해 보면 DDIM은 50보다 적은 steps에서는 더 좋은 샘플 퀄리티를 보였지만 더 많은 steps을 사용하면 본 논문에서 제시한 방법이 더 좋은 샘플 퀄리티틀 보였다
일정한 stride로 timestep을 줄이는 해당 논문의 방식을 DDIM에 적용해 보았는데 성능이 크게 하락하여 DDIM 논문에서 제시한 본래 방식을 사용하였다. 반대로 DDIM의 quadratic striding 방식을 본 논문의 방식에 사용해 보았는데 cosine schedule과 quadratic striding의 조합은 샘플 퀄리티를 저하시켰다.
5. Comparison to GANs
likelihood가 mode-coverage를 유추할 수 있는 좋은 metric이지만 likelihood 기반 모델이 아닌 GAN에서는 이를 구할 수 없다.
대신 precision과 recall을 사용하여 BigGAN-deep과의 성능을 비교하였다.

위는 GAN의 평가지표로 쓰이는 Precision, Recall에 대한 간단한 그림으로 파란색은 target distribution, 빨간색은 모델이 예측한 predicted distribution이다.
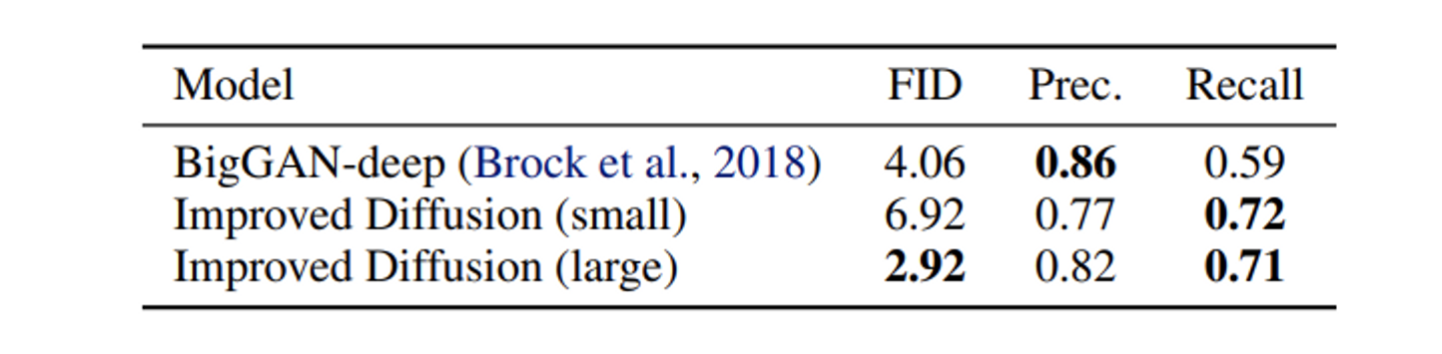
class-conditional model을 학습시켰는데 class embedding을 timestep embedding에 더하고 이를 model의 residual block에 주는 형식으로 conditional diffusion model을 설계하였다.
hybrid loss, 250 sampling steps을 공통으로 사용하였고 100M params, 1.7M steps 학습한 모델을 small, 270M params, 250K iterations 학습한 모델을 large 모델로 이름 붙였다.
BigGAN-deep은 100M params으로 구성하였으며 GAN, Improved-DDPM 모두 50K 개의 샘플을 생성하여 Precision, Recall을 측정하였다.
위 table을 보면 small 모델과 비교에서는 BigGAN이 FID, Precision에서 우세하나 Recall에서는 Improved-DDPM이 우세하였다.
large 모델은 FID, Recall에서 BigGAN을 크게 상회하였고 Precision 또한 비슷한 수준까지 달성하였다.
diffusion model은 GAN에 비해 높은 Recall을 보이는데 이는 diffusion model이 GAN에 비해 분포의 mode를 cover 하는데 더 뛰어나다는 것을 말한다.
6. Scaling Model Size
첫 layer의 channels이 64,96,128,192 일 때 모델의 성능을 측정하였다.
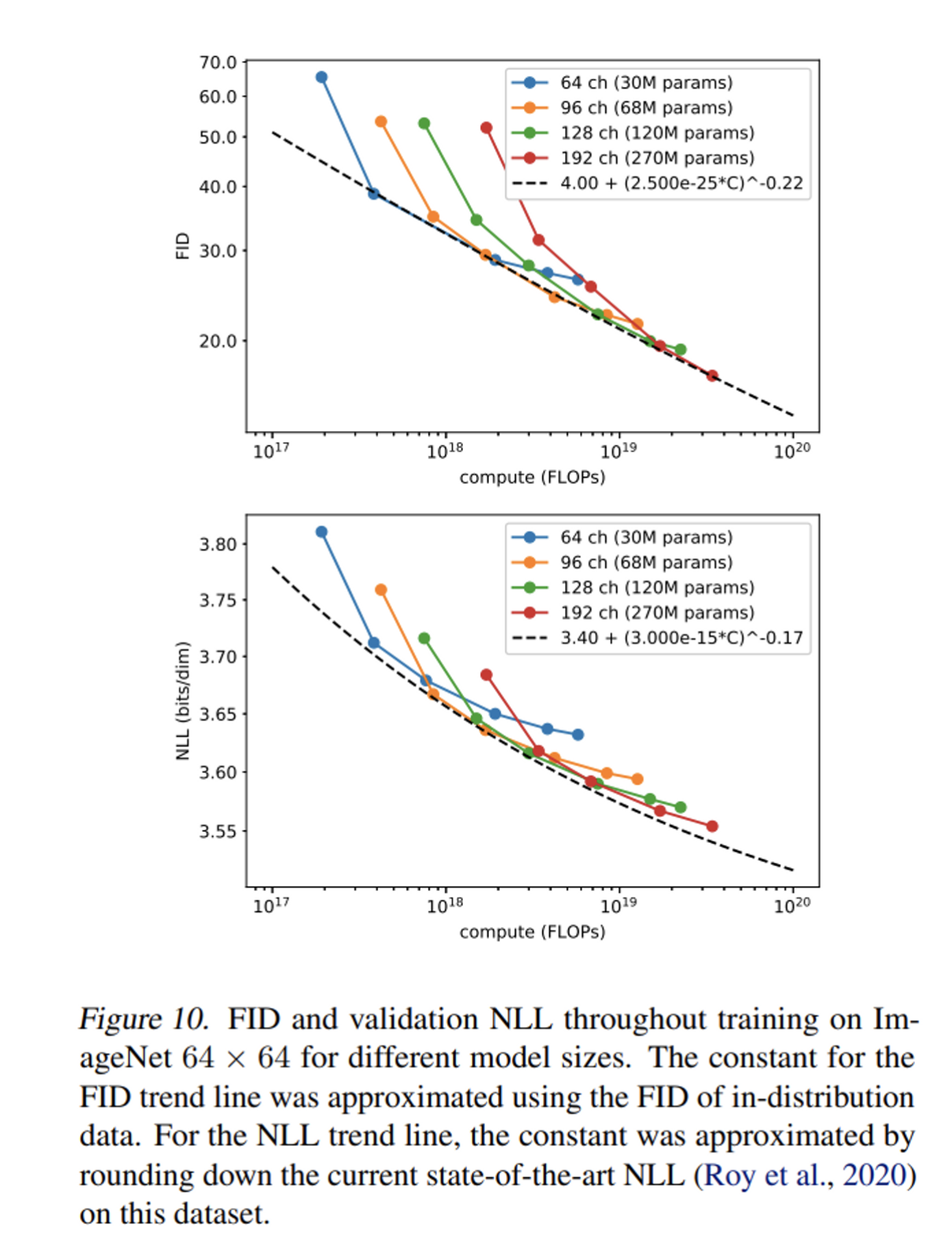
model size가 커짐에 따라 연산량이 클 때 성능이 더 좋아지는데 log-log plot에서 FID graph를 보면 거의 linear 하다는 것을 볼 수 있다. (scaling에 따른 성능 개선이 예측가능)
7. Conclusion
- DDPM을 개선해서 샘플 퀄리티 저하가 매우 작으면서도 더 빠르게 샘플링하고 더 좋은 log-likelihood를 달성한 Improved-DDPM을 제시
- Sigma를 학습하고 hybrid loss를 사용하는 것이 메인 아이디어로 이를 통해 다른 likelihood 기반 모델과 비슷한 수준의 likelihood를 달성
- 더 적은 샘플링 스텝으로도 퀄리티 좋은 샘플을 생성할 수 있다는 것을 발견
- DDPM은 GAN과 비슷한 샘플 퀄리티를 달성하면서도 mode-coverage에 뛰어나다는 것을 Recall을 통해 측정
- 더 많은 학습이 이루어지면 더 좋은 샘플 퀄리티, log-likelihood를 달성가능하다는 DDPM의 scalability에 대한 발견
- DDPM은 고품질의 샘플, 좋은 log-likelihood, 학습량 증가로 쉽게 scale 할 수 있는 정적인 training objective, 적당한 속도의 샘플링을 모두 갖춘 매력적인 generative model로 앞으로 유망한 연구 방향
후기 & 정리
- Sigmas 학습, vlb loss와 DDPM의 simplified loss를 합하여 만든 hybrid loss, cosine scheduling을 사용하여 DDPM의 log-likelihood와 sampling speed를 개선한 Improved-DDPM을 제시
- precision, recall을 사용한 BigGAN과 비교를 통해 diffusion 모델의 mode-coverage 성능을 측정
- 논문에서 제시하는 세팅(sigma learning, hybrid loss)에 대한 설명이 자세하게 되어있고 resampled hybrid loss, quadratic striding + importance sampling 등 좋은 성능을 기록하는 데에는 실패한 실험 또한 명시되어 있는 논문 (Appendix의 추가 실험들도 흥미로웠다)
- DDPM 논문의 발표 이후 어떻게 성능을 개선할 것인가를 고민하였던 것들이 보이고 재미있어서 핵심만 읽고 가려다가 끝까지 정독한 논문
Reference
[0] Alex Nichol et al., (2021), "Improved Denoising Diffusion Probabilistic Models", https://arxiv.org/abs/2102.09672
Improved Denoising Diffusion Probabilistic Models
Denoising diffusion probabilistic models (DDPM) are a class of generative models which have recently been shown to produce excellent samples. We show that with a few simple modifications, DDPMs can also achieve competitive log-likelihoods while maintaining
arxiv.org
'AI > Deep Learning' 카테고리의 다른 글
| Score-based Generative Models과 Diffusion Probabilistic Models과의 관계 (0) | 2023.05.16 |
|---|---|
| Diffusion Models Beat GANs on Image Synthesis (0) | 2023.05.05 |
| DDIM: Denoising Diffusion Implicit Models (0) | 2023.04.14 |
| Diffusion Model 수식 정리 (0) | 2023.04.08 |
| DDPM: Denoising Diffusion Probabilistic Models (0) | 2023.01.20 |




