| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Few-shot generation
- Stat110
- 디퓨전모델
- cv
- BERT
- multimodal
- userwidget
- UE5
- Diffusion
- CNN
- dl
- 딥러닝
- 언리얼엔진
- WBP
- GAN
- RNN
- motion matching
- Generative Model
- 오블완
- 폰트생성
- ue5.4
- WinAPI
- deep learning
- 모션매칭
- Font Generation
- ddpm
- animation retargeting
- Unreal Engine
- 생성모델
- NLP
- Today
- Total
Deeper Learning
Score-based Generative Models과 Diffusion Probabilistic Models과의 관계 본문
Score-based Generative Models과 Diffusion Probabilistic Models과의 관계
Dlaiml 2023. 5. 16. 21:42Generative Modeling by Estimating Gradients of the Data Distribution
https://arxiv.org/abs/1907.05600
Score-based Generative Model의 개념을 소개한 논문
Given this dataset, the goal of generative modeling is to fit a model to the data distribution such that we can synthesize new data points at will by sampling from the distribution.
생성모델에서 목표는 주어진 데이터셋을 활용하여 모델이 데이터 분포를 실제 데이터 분포와 가깝게 근사하고 구한 데이터 분포를 활용하여 새로운 데이터를 샘플링 하는것이다.
MNIST 데이터를 예로 들면 데이터 공간상에서 높은 확률값에 해당하는 이미지는 검은 배경에 흰 색으로 쓰여있는 0~9의 숫자 이미지일 것이며 낮은 확률값에 해당하는 이미지는 의미없는 Noise일 것이다.

위 그림은 MNIST 데이터 분포의 가상의 probability density funciton(이하 pdf)로 pdf의 기울기를 계산할 수 있으면 그것을 활용하여 확률값이 높아지는 방향으로 데이터를 업데이트하여 실제 데이터셋과 유사한(높은 확률값에 해당하는) 데이터를 생성할 수 있다.
Score란?
Score는 pdf의 미분으로 정의된다. (입력 데이터 x에 대한 미분)
다변량 가우시안 분포에서 이를 구해보면 pdf

log를 씌우고 로 미분한 값은 아래와 같다

Data samples을 가지고 Score를 추정하고(Score matcing), 추정된 score 값들을 바탕으로 새로운 샘플을 생성하는 것(Langevin dynamic)이 Score-based Generative Models의 원리이다.
위 다변량 가우시안 예시는 실제 데이터의 분포를 알고 있기 때문에 미분을 통해 모든 data point에서 score를 구할 수 있었는데 현실에서 문제는 데이터의 분포를 알고 있지 않다는 것이다. (알고 있다면 이미 해결된 문제)

Score Matching(2005)는 score를 다시 미분한 Jacobian Matrix를 활용하여 Score Network가 True Score를 근사하도록 한 방식인데, score의 dimension이 커지면서 계산이 어려워진다는 문제가 존재했다.
2011년에는 Score를 학습하기 위한 새로운 score matching 방식인 Denoising Score Matching이 공개되었다.
Denoising score matching은 데이터에 가우시안 노이즈를 추가한 후 score를 예측하는 방식으로 noise가 충분히 작다면 원래 데이터의 score와 가까운 값을 구할 수 있다는 점을 활용하였다.
위 식에서 는 가우시안 노이즈, 는 가우시안 노이즈가 추가된 데이터를 말한다.
Score Network는 Score를 추정하는 Network로 논문에서는 U-Net 구조를 사용하였다. 원본 데이터에 noise를 더하고 Score Network에 통과시켜 나온 output과 Score의 L2 loss를 objective로 사용한다.
Denoising score matching의 장점 중 하나는 Score의 미분하기전 식이 가우시안 노이즈라서 계산이 간편하다는 것.
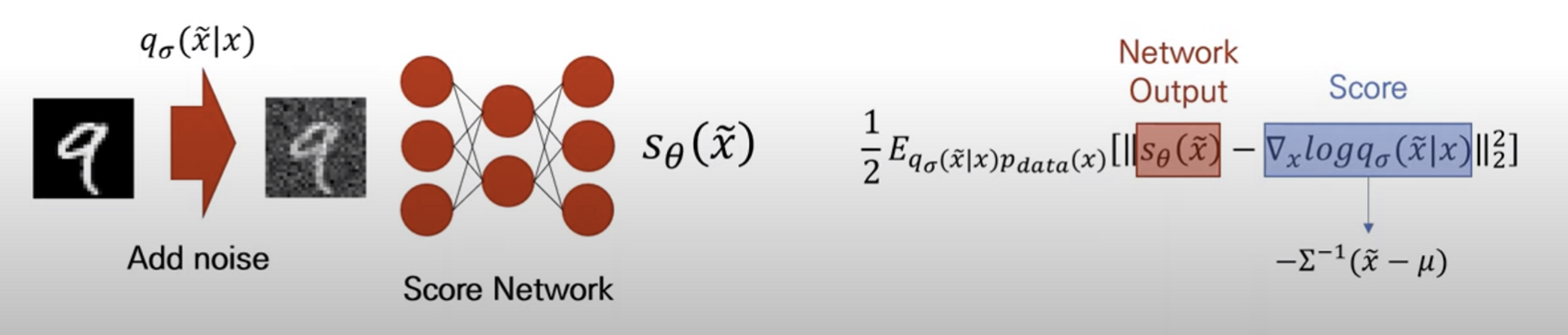
Score-based model 를 학습하였으면 이제 Langevin Dynamics을 사용해서 샘플을 생성할 수 있다. Langevin Dynamics은 분포 와 분포의 score function 만 사용하여 MCMC procedure로 sampling하는 방식으로 임의의 prior distribution 에서 시작하여 아래 식을 반복한다. .
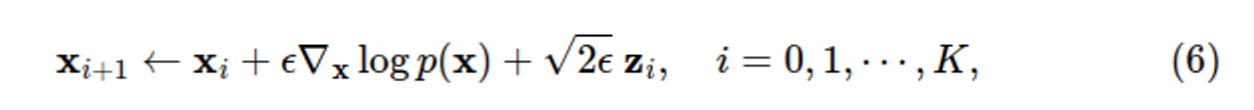
이면 위 식을 반복하여 얻은 데이터는 regularity condition이 있다면 샘플링한 데이터에 수렴하게 된다.

하지만 위 방식에는 문제가 있는데, score model과 true score 간 l2 differences는 에 의해 가중치가 주어지는 점이다.
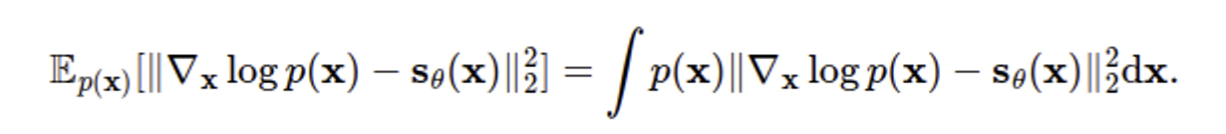
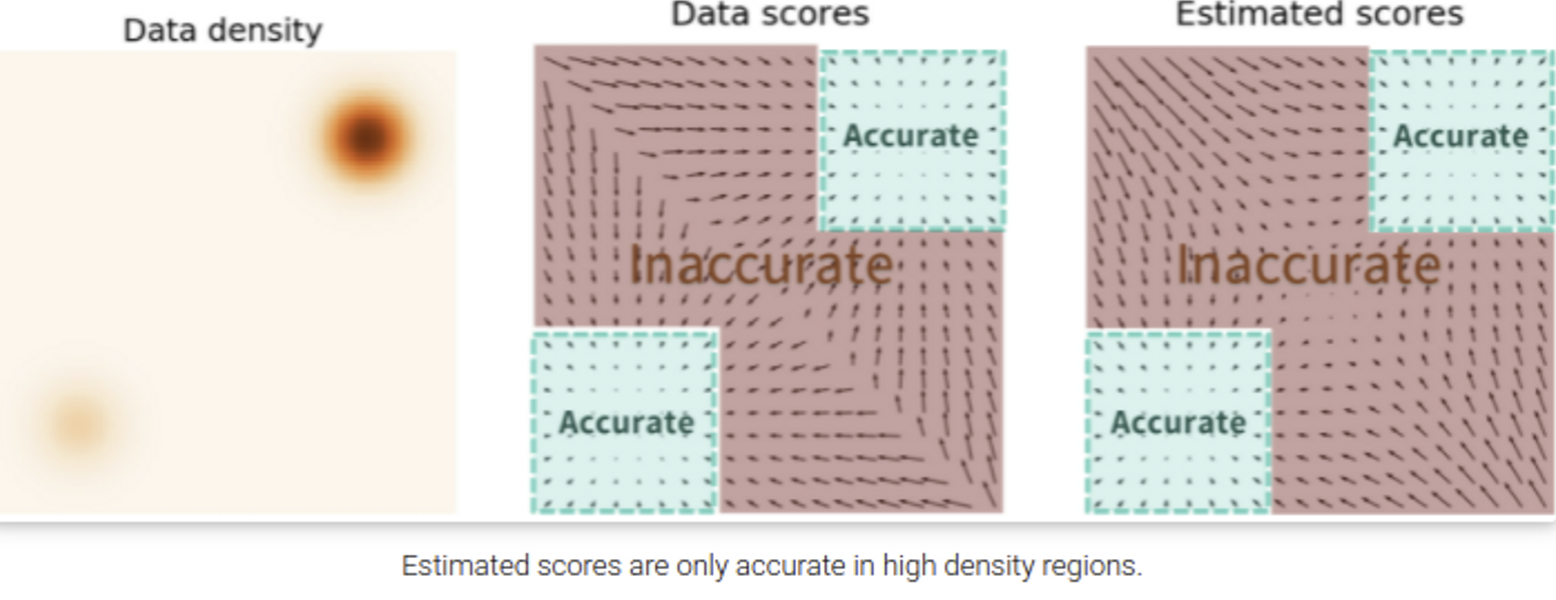
즉, 데이터가 적은 영역에 대해서는 아래 그림과 같이 정확하게 score model에 score function을 예측하지 못할 가능성이 크다. 그리고 매니폴드 가설에서 대부분 영역은 대부분 데이터는 비교적 작은 차원의 영역에 집중되어 있어 정확한 score를 예측할 수 없는 영역이 매우 크다.
이를 해결하기 위해 데이터에 noise를 추가하는 방식이 제안되었다. noise가 추가되면 아래 그림과 같이 데이터가 영향을 끼치는 영역이 늘어나 비교적 데이터가 적었던 영역에서도 더 정확한 score function의 추정이 가능하다.
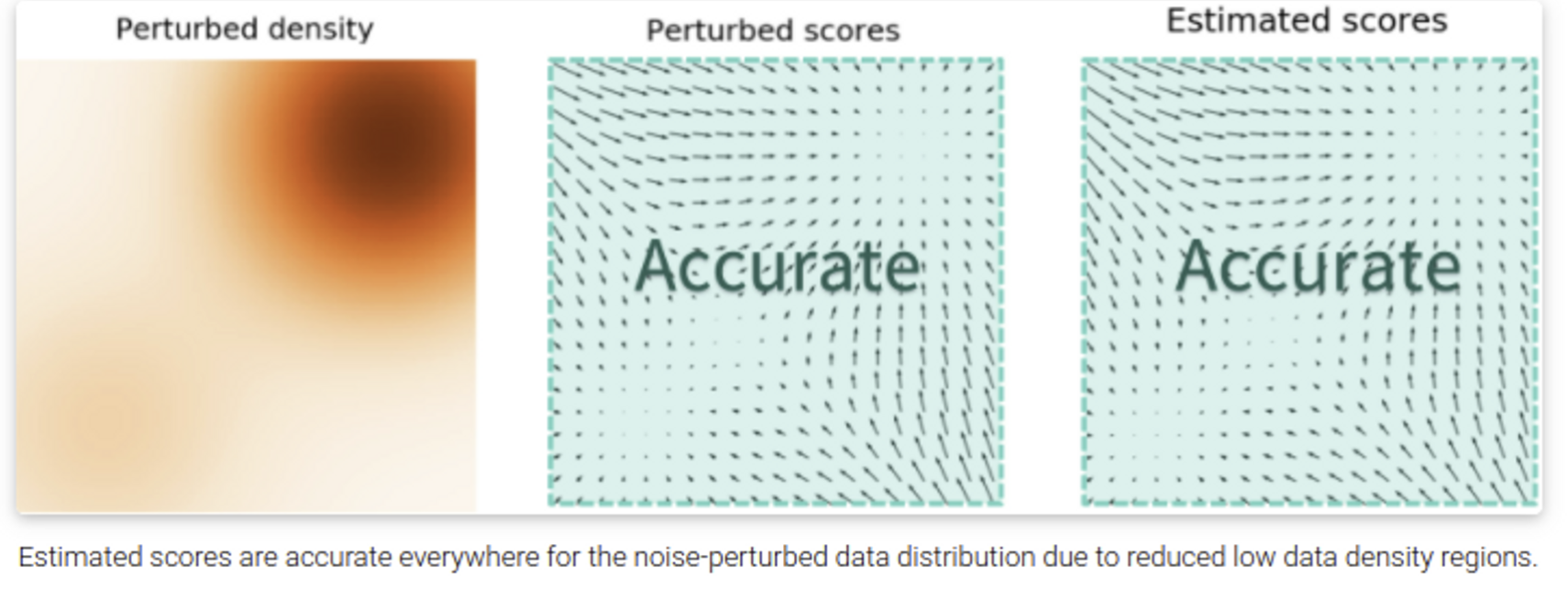
noise를 condition으로 추가한 위 방식을 Noise Conditional Score Networks라고 하며 줄여서 NCSN으로 부른다.

Noise를 점점 줄이며 단계적으로 샘플링하는 Annealed Langevin dynamics으로 샘플링이 가능하다.

정리해보면 Score-based Generative Models 논문에서 제시한 모델은 Score matching을 위해 Noise Condition Score Network(NCSN)을 사용하였고 샘플 생성을 위해 Annealed Langevin Dynamics를 사용한 모델이다.
Diffusion Probabilistic Models & Score-based Generative Models
Diffusion 확률 모델(이하 DPM)과 앞서 살펴본 Score-based Generative Model(이하 score-based model)이 꽤 유사해보이는데, 데이터를 multiple scale noise로 perturb하고 denoise하는 방식으로 샘플을 얻는다는 공통점이 있다. 하지만 DPM은 ELBO를 사용하여 학습하고 학습된 decoder를 사용하여 샘플링하며 Score-based model은 score matching objective를 사용하여 학습, Langevin dynamics을 사용하여 샘플링한다는 차이가 있다.
후에 2020년에 나온 논문인 DDPM은 score-based model과 DPM의 깊은 연관성에 대해 연구하였는데 DPM을 학습하기 위해 사용하는 ELBO가 score-based model에서 사용하는 score matching objective의 가중치를 주고 조합한 것과 동일하다는 것을 밝혔다. decoder를 U-Net 아키텍처를 사용하여 score-based model의 sequence로 parameterize하여 DPM이 GAN의 샘플 퀄리티를 넘어서는 성과를 낼 수 있음을 보였다.
Yang Song(Score-based model 저자)는 DDPM에서 영감을 받아 DPM과 score-based model의 관계를 더 조사하였고 이를 담은 논문인 Score-Based Generative Modeling through Stochastic Differential Equations을 2021년에 제출하였다.
저자는 DPM의 샘플링 방식을 score-based model의 Annealed Langevin dynamic과 결합하여 통합된 강력한 sampler(the Predictor-Corrector sampler)를 만들 수 있음을 발견하였다. 또 noise scale의 총 개수를 무한으로 늘리면 DPM과 score-based model 모두 score function에 의해 정의되는 stochastic differential equations의 이산화로 볼 수 있다는 것을 증명하였고 score-based model과 DPM을 하나의 프레임워크로 연결하였다.
최신 연구들은 DPM과 score-based model이 동일한 model family의 다른 관점이라는 것을 밝히는데까지 성공하였다.
Stochastic differential equations
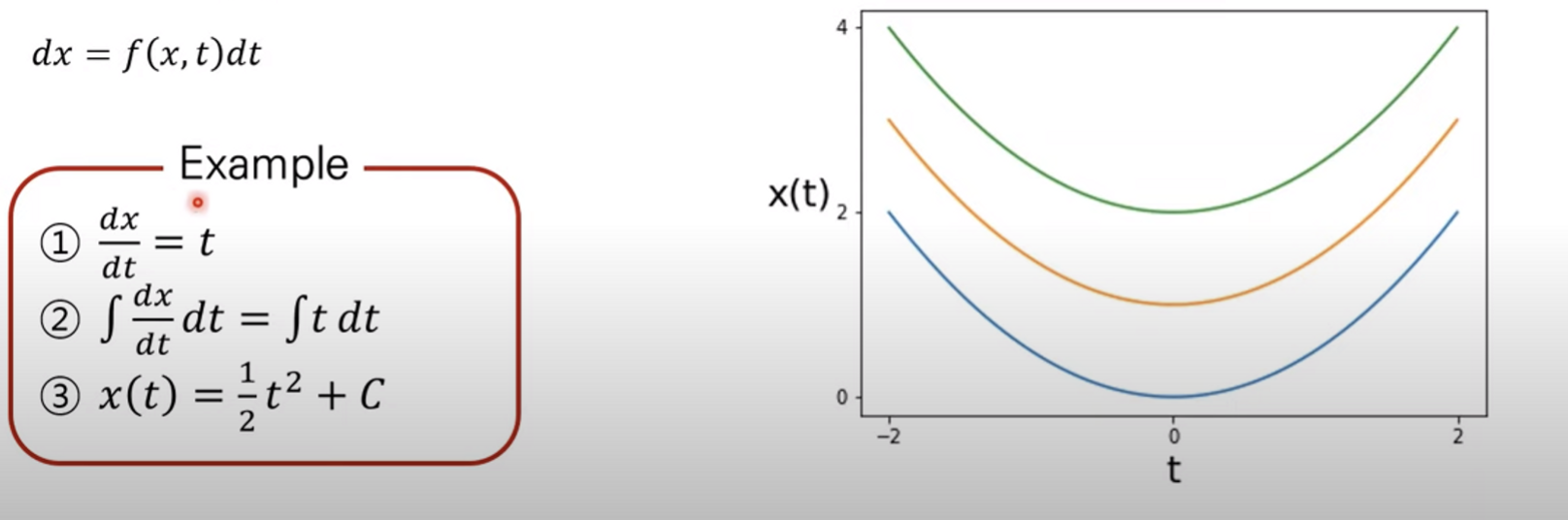
간단한 미분방정식 개념을 다시 복습해보자.
ODE(Ordinary Differential Equation)는 최종적으로 t에 따른 를 구한다
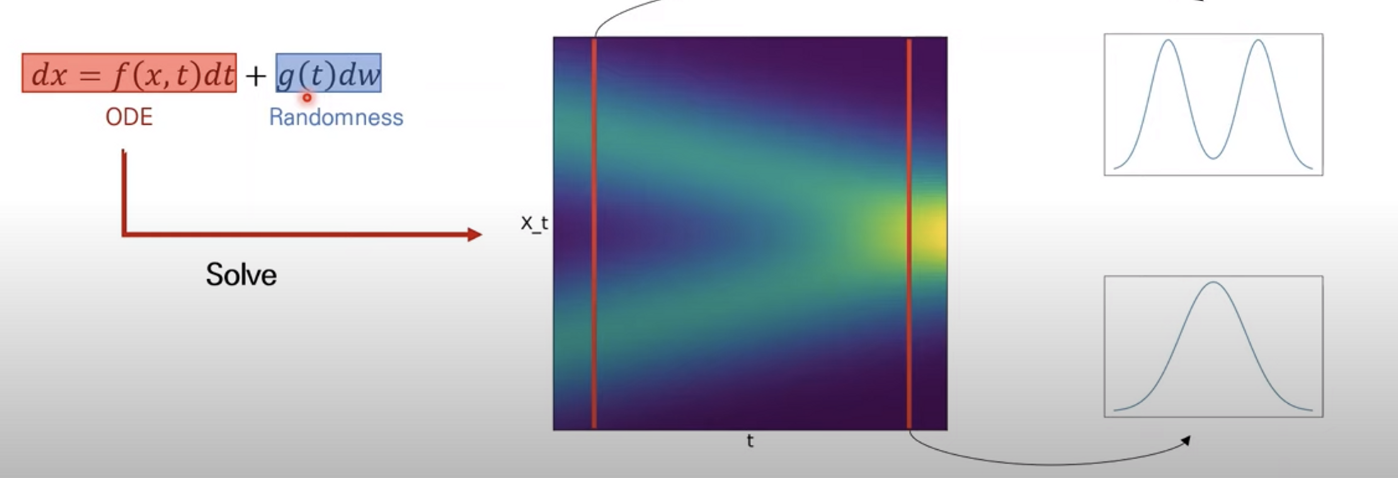
SDE는 여기에 추가로 randomness가 추가된다. SDE를 푼다는 것은 최종적으로 모든 t에 따른 Random process를 찾는것이다. timestep t에서 x의 marginal distribution을 구하는 것.
Score-based Generative Modeling with SDEs
(간단하게 개요만 설명, 해당 논문은 후에 따로 포스팅 예정)
noise scale의 수가 무한에 가까워지면 continuous하게 증가하는 noise를 데이터에 줄 수 있고 아래 그림과 같이 noise perturbation process는 continuous-time stochastic process가 된다.


NCSN/DDPM에 continuous한 noise scale 수를 적용시키면 SDE 프레임워크 관점으로 볼 수 있는데, 그러면 noise를 추가하는 과정은 Forward SDE, Reverse SDE는 noise를 제거하는 과정으로 볼 수 있다 (SDE는 상응하는 reverse SDE를 항상 가지고 있다)

NCSN, DDPM의 forward SDE 수식을 보면 (continuous timestep을 적용한 결과)
NCSN은 timestep이 증가함에 따라 variance가 점점 커지는 Variance Exploding SDE(VE-SDE), DDPM은 분산이 유지되는 Variance Preserving SDE로 부를 수 있다.
SDE 관점으로 NCSN, DDPM을 보면 이제 샘플링은 reverse SDE를 푸는것과 같기 때문에 전통적인 방식인 Euler-Maruyama, Runge-Kutta와 같은 방식을 사용할 수 있게된다.
논문에서는 Predictor: Reverse SDE를 풀어 데이터 생성, Corrector: Predictor에서 생성된 데이터에 Annealed Langevin dynamics를 사용하는 Predictor, Corrector Sampler를 제시하였다.
(추가 설명)

정리
- p.d.f의 미분값을 score function으로 정의하고 여러 score matching 방법론을 통해 True score function을 추정하고 Langevin dynamics등을 사용하여 샘플링하는 score network Score-based Generative Model에 대해 알아보았다.
- multiple scale의 noise로 데이터를 perturb하고 denoising score matching, Annealed Langevin Dynamics으로 샘플링하는 NCSN에 대해 알아보았다.
- NCSN, DDPM의 timestep을 연속적인 값으로 설정하고 SDE 관점으로 이 둘을 각각 VE-SDE, VP-SDE로 보았으며 SDE Solver로 얻은 trajectories(Predictor)를 MCMC 방식으로 fine-tune(Corrector)하는 Predictor-Corrector samplers에 대해 알아보았다.
Reference
https://yang-song.net/blog/2021/score/
https://www.youtube.com/watch?v=d_x92vpIWFM
https://www.youtube.com/watch?v=yqF1IkdCQ4Y&list=PLVP0u2f6ruB9hi55ufLViYSgKti1GHyzp&index=8
'AI > Deep Learning' 카테고리의 다른 글
| LDM: High-Resolution Image Synthesis with Latent Diffusion Models (0) | 2023.06.02 |
|---|---|
| Score-Based Generative Modeling through Stochastic Differential Equations (0) | 2023.05.27 |
| Diffusion Models Beat GANs on Image Synthesis (0) | 2023.05.05 |
| Improved-DDPM: Improved Denoising Diffusion Probabilistic Models (0) | 2023.04.19 |
| DDIM: Denoising Diffusion Implicit Models (0) | 2023.04.14 |




