| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- Stat110
- motion matching
- 폰트생성
- ue5.4
- deep learning
- UE5
- 생성모델
- 오블완
- WinAPI
- cv
- CNN
- 모션매칭
- GAN
- dl
- ddpm
- Few-shot generation
- WBP
- BERT
- RNN
- animation retargeting
- 언리얼엔진
- Generative Model
- userwidget
- NLP
- Unreal Engine
- Diffusion
- 딥러닝
- Font Generation
- multimodal
- 디퓨전모델
Archives
- Today
- Total
Deeper Learning
VQ-VAE: Neural Discrete Representation Learning 본문
Aaron van den Oord, Oriol Vinyals, Koray Kavukcuoglu, Deepmind. (2017.11)
Abstract
- unsupervised로 유용한 representation을 학습하는 것은 머신러닝에서 쉽지 않다
- discrete representation을 학습하는 간단하고 강력한 generative model: Vector Quantised Variational Autoencoder(VQ-VAE)를 제시
- encoder의 output이 discrete, prior가 static이 아닌 학습된다는 점이 VAE와의 차이점
- discrete representation 학습을 위해 vector quantisation(이하 VQ)을 활용
- VQ는 posterior collapse를 우회할 수 있음
- posterior collapse: input → posteiror parameter의 정보가 약하거나 noisy 할 때 발생, powerful AR decoder가 posterior qϕ(z|x)를 무시하고 생성, qϕ(z|x)≈q(z)
- VQ-VAE는 high-quality의 이미지, 비디오, 음성을 생성할 수 있음
Introduction
- Maximum likelihood와 reconstruction error는 pixel domain에서 unsupervised model을 학습시킬 때 보편적으로 사용하는 objectives
- 목표는 latent space 내에 중요한 features를 보존하면서 maximum likelihood를 optimising
- Kingma는 “Variational Lossy Autoencoder”논문에서 best 생성 모델은 latent 없이 PixelCNN과 같은 powerful decoder라고 하였으나 저자는 discrete, useful 잠재 변수의 학습을 주장
- discrete features는 우리가 관심있어하는 domain에 더 자연스럽게 맞아떨어진다
- Language: 내재적으로 discrete
- speech: symbols의 sequence
- Image: language로 간결하게 묘사 가능
- discrete latent variables을 딥러닝에서 활용하기는 어렵지만 poweful autoregressive models에서는 분포 모델링이 가능
- VQ-VAE는 VQ를 활용하여 학습이 간단하며 large variance에 문제를 덜 겪으며 posterior collapse를 피할 수 있다
- VQ-VAE는 continuous latent variables을 사용하는 모델과 비슷한 성능을 보인 첫 discrete latent VAE 모델로 이는 discrete distribution의 flexibility를 뒷받침
- VQ-VAE는 latent space를 효과적으로 사용하기 때문에 local한 noise나 매우 사소한 detail에 capacity를 낭비하지 않고 data space의 많은 차원을 span하는 중요한 feature를 성공적으로 모델링할 수 있다.
contributions
- 간단하고 discrete latents를 사용하며 posterior collapse, variance issues를 피할 수 있는 VQ-VAE를 제시
- log-likelihood 기준 상응하는 continuous model과 비슷한 성능을 discrete latent model로 달성
- powerful prior와 함께 사용하면 speech, video 생성과 같이 다양한 분야에서 일관적이고 높은 퀄리티 샘플을 생성
- supervision 없이 raw speech에서 language를 학습, 이를 사용하여 unsupervised speaker conversion 성공
Related Work
- discrete VAEs training: NVIL, VIMCO
- new reparametrization based on Concrete, Gumbel-softmax distribution
- compression using VQ
VQ-VAE
prior, posterior distribution은 categorical, distribution에서 뽑은 샘플들은 embedding table의 index이며 이렇게 찾은 embedding이 decoder network의 input이 되는 형태
Discrete Latent variables
- latent embedding space를 e∈RK×D로 정의, K는 discrete latent space size, D는 각 latent embedding vector ei의 dimensionality
- K개의 embedding vector 존재 (ei∈RD,i∈1,2,...,K)

- input x는 위 그림과 같이 encoder를 통과하여 output ze(x)가 됨

- discrete latent variables z는 위와 같은 수식으로 nearest neighbour를 사용하여 선택된다
- decoder의 input은 위에 선택된 ze(x)의 nearest neighbour ej, zq(x)=ek
Learning
- nearest neighbour로 ej를 선택할 때 미분 불가능한 연산으로 gradient가 흐르지 않는다
- straight-through estimator와 같이 gradient 근사를 사용
- 간단하게 decode input zq(x)의 gradient를 ze(x)로 copy
- quantisation을 사용하여 subgradient를 활용할 수 있으나 간단한 copy 방식도 실험적으로 잘 작동하였음
- encoder의 output과 decoder의 input은 같은 D dimensional space를 사용하기 때문에 encoder에도 유용한 gradient를 전달할 수 있음
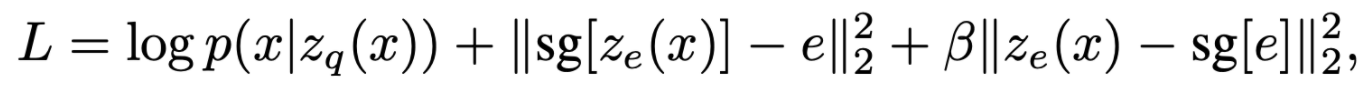
- 전체 Loss term은 위와 같으며 첫째 항은 reconstruction loss로 decoder와 encoder의 parameters를 update
- 하지만 reconstruction loss로는 embedding space ej를 update 할 수 없고(straight-through gradient) ej를 update하기 위해 간단한 dictionary learning algorithms, Vector Quantisation(VQ)를 사용
- sg는 stopgradient operator로 forward propagation 때는 계산은 일반적인 상황과 동일하나 partial derivatives를 0으로 만듦 (gradient=0)
- second term은 e가 encoder output ze(x)와 가까워지도록 하는 l2 loss
- last term은 Commitment loss로 embedding space의 volume이 dimensionless이며 encoder의 parameter 만큼 빠르게 ej가 학습되지 못할 경우 크기가 임의로 커질 수 있기 때문에 encoder 출력이 embedding space와 가까워지도록 해주는 loss (β 는 0.1~2.0이 적절, 논문에서는 0.25를 사용)
- complete model logp(x)의 log-likelihood는 아래와 같이 표현할 수 있다
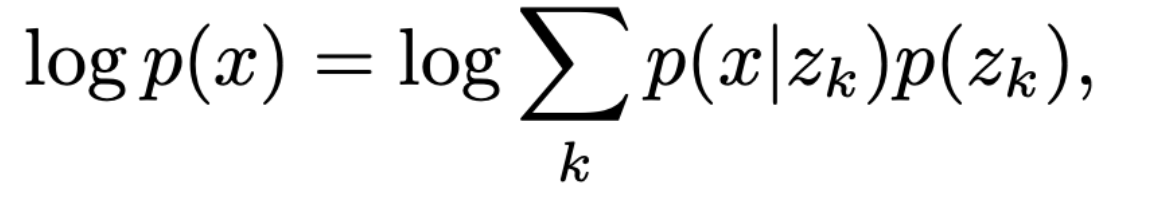
- decoder p(x|z)는 MAP 추론 관점으로 보면 z=zq(x)로 학습되었기 때문에 식을 아래처럼 다시 쓸 수 있다. (Jensen’s inequality를 적용하여 부등호를 사용할 수 있다)
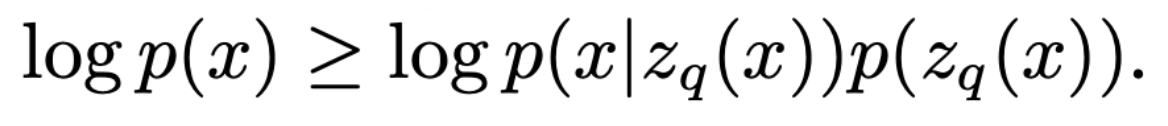
Prior
- discrete latents p(z)의 prior distribution은 categorical distribution이며 feature map의 다른 z에 따라 autoregressive하게 만들 수 있음
- VQ-VAE가 학습 중일 때 prior는 constant, uniform으로 유지하지만, 학습이 끝나고 autoregressive distribution을 z에 fit하여 ancestral sampling으로 x를 생성
- PixelCNN, WaveNet 등을 prior 학습에 사용
- prior와 VQ-VAE의 동시 학습을 future work으로 제시
Experiments

- ImageNet의 reconstruction 결과로 discrete latent로 정보 압축에 성공함을 볼 수 있다
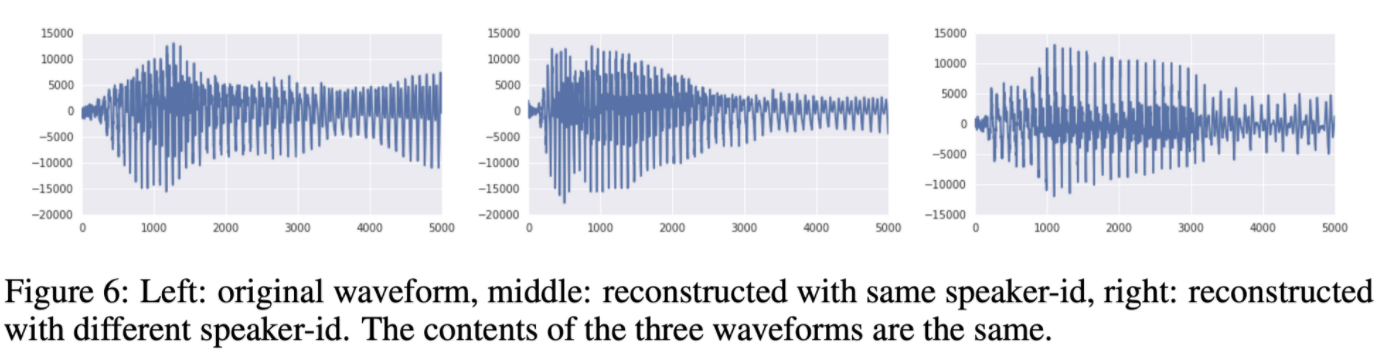
- VQ-VAE로 음성 데이터를 long-term relevant information만 보존하도록 latent를 설정하고 decoder로 reconstruction을 학습하면 말하는 내용은 그대로인 상태로 높낮이만 바뀌는 형태로 reconstruction이 가능
- 이는 VQ-VAE가 supervision없이 data space를 이해하고 speech의 content만 encode
- unsupervised 화자 바꾸기도 speaker one-hot information을 활용하여 가능
Conclusion
- vector quantisation으로 얻은 discrete latent representation을 사용하는 VAE인 VQ-VAE를 제시
- VQ-VAE는 unsupervised manner로 data의 중요한 features를 encoding 할 수 있음
- continuous latent representation과 비슷한 성능을 보여줌
정리 & 후기
- 상응하는 아키텍처의 continuous latent VAE와 비슷한 성능을 보여주는 discrete latent를 사용하는 VQ-VAE를 제시
- Real world의 여러 데이터들은 discrete features로 표현할 수 있음
- discrete latent를 사용하는 VAE 학습에 성공한 모델이라는 것 자체가 의의
- VQ-VAE는 DALL-E에도 사용되는 활용성이 높은 모델
Reference
[0] Aaron van den Oord et al. (2017). “Neural Discrete Representation Learning”. https://arxiv.org/abs/1711.00937
'AI > Deep Learning' 카테고리의 다른 글
| ALBERT: A Lite BERT for Self-supervised Learning of Language Representations (0) | 2022.06.05 |
|---|---|
| RoBERTa: A Robustly Optimized BERT Pretraining Approach (0) | 2022.06.01 |
| f-GAN: Training Generative Neural Samplers using Variational Divergence Minimization (0) | 2022.04.07 |
| GAN: Generative Adversarial Nets (0) | 2022.03.28 |
| Font Generation with Missing Impression Labels (0) | 2022.03.23 |




