| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- ddpm
- Unreal Engine
- cv
- dl
- 폰트생성
- 모션매칭
- WBP
- ue5.4
- Few-shot generation
- 생성모델
- Font Generation
- deep learning
- UE5
- WinAPI
- animation retargeting
- multimodal
- NLP
- 디퓨전모델
- userwidget
- Stat110
- CNN
- 언리얼엔진
- BERT
- 딥러닝
- 오블완
- Diffusion
- GAN
- RNN
- Generative Model
- motion matching
Archives
- Today
- Total
Deeper Learning
f-GAN: Training Generative Neural Samplers using Variational Divergence Minimization 본문
AI/Deep Learning
f-GAN: Training Generative Neural Samplers using Variational Divergence Minimization
Dlaiml 2022. 4. 7. 13:20Sebastian Nowozin, Botond Cseke, Ryota Tomioka. (2016)
Abstract
- Generative neural sampler는 feedforward NN을 통해 샘플링하는 probabilistic model
- sampling과 도함수를 쉽게 계산할 수 있지만 likelihood, marginalization을 계산할 수 없음
- generative-adversarial approach가 더 일반적인 variational divergence estimation approach의 special case임을 논문에서 제시
- 모든 f-divergence를 generative neural sampler를 학습시킬 때 사용할 수 있음
- 다양한 divergence function을 사용하는 것의 complexity 학습에서의 장점, 학습된 생성 모델의 퀄리티 측면에서 장점에 대해 다룰 것이다
1. Introduction
- Probabilistic generative model은 주어진 도메인 X에서 확률분포를 표현한다
- possible model class Q에서 generative model q가 주어졌을 때, 보통 다음과 같은 operations에 관심이 있다
- Sampling: sample을 q에서 생성. sample에 대한 분석, sample set에 대한 functionsn 계산을 통해 decision problem을 풀거나 분포에 대한 중요한 insight를 얻을 수 있다.
- Estimation: unknown true distribution P에서 얻은 i.i.d samples set {x1,x2,...,xn}로 true distrubution을 가장 잘 describe 하는 q를 찾기
- Point-wise likelihood evaluation: sample x에서 likelihood q(x)를 evaluate
- GAN은 간단한 분포에서 sampling한 random number vector를 input으로 하는 fedforward NN을 사용하며 정확한 sampling과 approximate estimation이 가능
- GAN은 한번의 forward pass로 하나의 sample을 만들 수 있는 효과적인 구조
- probabilistic feedforward NN models을 generative neural sampler라고 이름 붙임 (GAN도 이에 속함)
- GAN을 제시한 논문에서 저자는 symmetric Jensen-Shannon divergence를 approximate minimization으로 neural samplers를 추정할 수 있음을 보였다

- GAN 학습의 주요 테크닉은 동시에 최적화되는 두번째 NN인 “discriminator”를 도입한 것
- DJS(P||Q)가 적절한 분포 간 divergence measure이기 때문에 이는 true distribution P가 충분한 training samples이 있고 model class Q가 P를 표현할 수 있을 만큼 가까울 경우 P를 근사할 수 있음을 뜻함
- GAN의 principle이 더 일반적이고 Nguyen et al.이 제안한 variational divergence estimation framework를 확장하여 GAN training objective를 복구하고 이를 임의의 f-divergences로 일반화할 수 있음을 논문에서 보임
- contributions
- GAN training 목적 함수를 모든 f-divergences에 대해 유도하고 Kullback-Leibler, Pearson divergences 등과 같은 divergence를 추가 예시로 제시
- Goodfellow et al.의 saddle-point optimization 과정을 단순화, 이론적 증명
- natural image에 대해 generative nerual samplers를 추정하는 데 어떤 divergence가 적합한지 insight 제시
2. Method
먼저 Nguyen et al.이 제시한 f-divergence 기반 divergence estimation framework에 대해 살펴보고 이를 model estimation으로 확장하겠다
2.1. The f-divergency Family
- Kullback-Leibler divergence와 같은 통계적 divergence는 두 확률분포의 차이를 측정한다
- 다양한 divergences의 large class를 f-divergence 또는 Ali-Silvey distance라고 한다
- 두 분포 P,Q의 domain X에서 연속적인 density function p,q에 대해 f-divergence
- generator function f:\R+→\R (positive real → real)가 convex
- f(1)=0을 만족하는 lower-semicotinuous function
- 위 2가지 조건을 만족할 때 f-divergence는 아래와 수식과 같이 정의된다

2.2. Variational Estimation of f-divergence
- Nguyen et al.은 P,Q의 sample에서 f-divergences를 추정하는 일반적인 variational method를 유도
- 저자는 이를 고정된 모델에서 parameters를 추정하도록 확장한 새롭게 제시한 method를 variational divergence minimization(VDM)이라 이름 붙임
- generative-adversarial training은 VDM의 special case
- 모든 convex, lower-semicontinuous 함수 f는 convex conjugate function f∗ (Fenchel conjugate)를 가지며 수식은 아래와 같음

- conjugate function의 특성으로 f의 convexity에 관계없이 f∗는 convex, f와 같이 lower-semicontinous
- f∗,f는 dual로 f∗∗=f이므로 f를 아래와 같이 다시 나타낼 수 있다

- Nguyen et al.은 위 수식을 활용하여 divergence의 lower bound를 구하였다 (τ는 functions \Tau:X→\R의 arbitrary class)
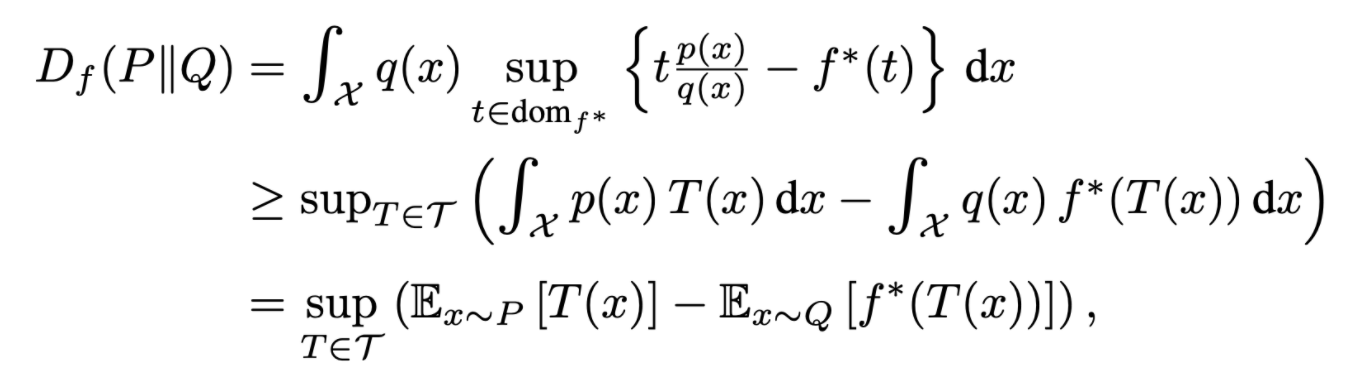
- 수식의 전개는 duality 활용 → Jensen’s Inequality
- 해당 유도한 lower bound를 maximize 하는 식으로 optimization 가능 (아래 mild condition을 만족하면 bound가 tight)
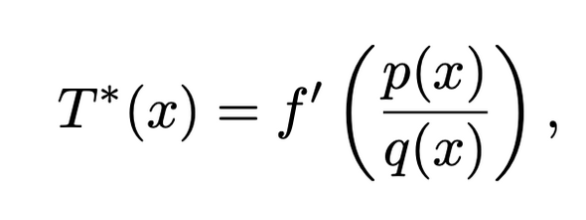
- 예시로 reverse Kullback-Leibler는 generator function은 f(u)=−log(u), T∗(x)=−q(x)/p(x)를 만족하는 식이 함수 class
해석
- 수식을 잘 보면 lower bound를 만드면서 Expectation 형태로 수식이 정리되어 분포를 알지 못하여도 sample을 가지고 계산하는 것이 가능해짐
- f-divergence를 추정하는 수식이 GAN의 목적함수와 비슷하게 정리되었음, 실제로 generator function 선정에 따라 vanilla GAN을 만들 수 있음
- GAN이 P,Q의 분포를 다루는 문제를 expectations을 다루는 쉬운 문제로 converter 역할을 하고 있었음

2.3. Variational Divergence Minimization (VDM)
- 이제 variational lower bound를 f-divergence Df(P||Q)에서 사용하여 주어진 true distribution P에서 generative model Q를 추정할 수 있다
- vector θ로 parameterize한 Qθ와 vector w로 parameterize한 \Tauw으로 generative-adversarial approach를 적용 가능 (Q는 생성모델, T는 sample → scalar)
- θ에 대해 minimize, w에 대해 maximize하는 f-GAN의 목적함수를 사용하여 saddle-point를 찾으며 생성모델 Qθ를 학습시킬 수 있다
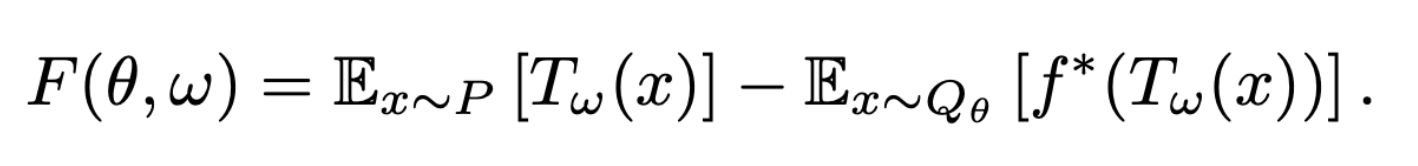
- 위 식을 optimize하기 위해 minibatch sample을 사용하여 expectations을 근사

2.4. Representation for the Variational Function
- 2.3에 제시된 수식을 다양한 f-divergence에 사용하려면 conjugate function의 dom에 대한 분석이 필요
- variational function \Tauw를 \Tauw(x)=gf(Vw(x)) form 으로 수정하여 식을 다시 쓰면 아래와 같다
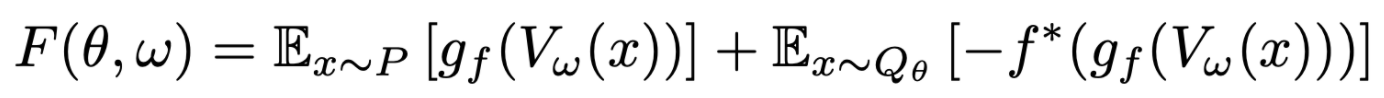
- Vw:X→\R은 output에 제약이 없으며, gf:\R→domf∗는 사용한 f-divergence에 따른 output activation function
- f-divergence와 그에 따른 output activation function
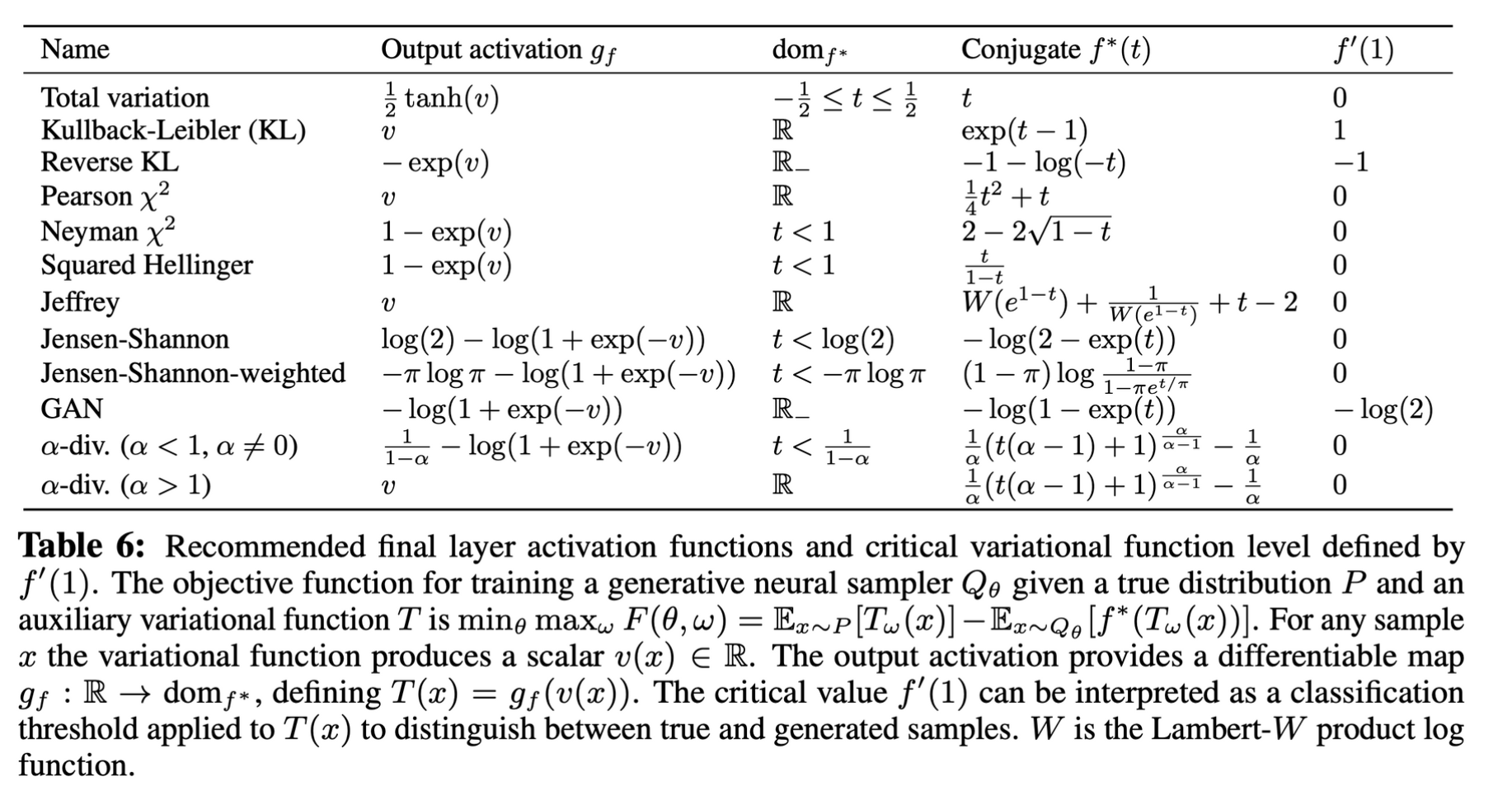
2.5. Example: Univariate Mixture of Gaussians
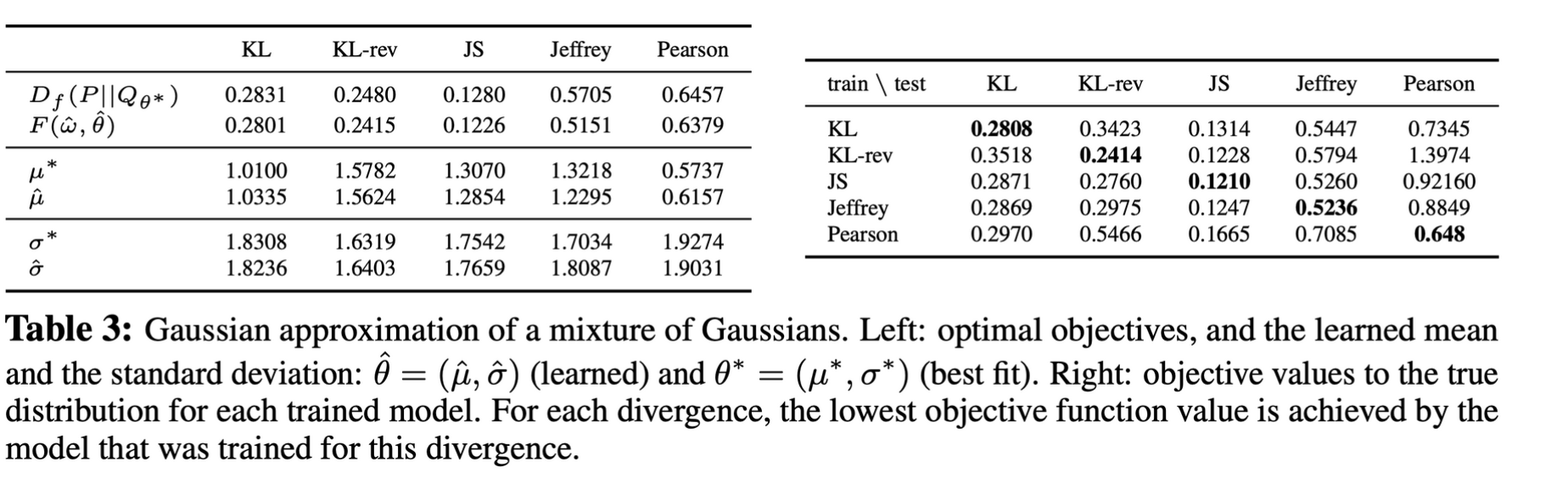
- true parameter set θ∗로 얻은 objective value와 그 lower bound를 optimize하며 학습한 parameter set ˆθ의 obejctive value 비교: 차이가 크지 않도록 잘 학습되었음
- 우측의 표는 train, test divergence를 다르게 하여 측정한 값들, 학습 때 목표로 한 divergence에 대해 optimize가 된 것을 확인할 수 있음
- generative model이 true distribution을 근사하지 못할 때 divergence function의 선택이 이에 영향을 크게 미칠 수 있음을 시사
3. Algorithms for Variational Divergence Minimization (VDM)
objective의 saddle point를 찾기 위한 method
- Goodfellow가 제안한 alternating method
- 더 직접적인 single-step 최적화 procedure
논문에서 제시한 variational framework에서 alternating method는 internal loop는 divergence의 lower bound를 조여주고 outer loop는 generator model을 향상시키는 double-loop 방식
3.1. Single-Step Gradient Method

- inner loop가 없음
- saddle point 주변에서 saddle point에 수렴함을 증명
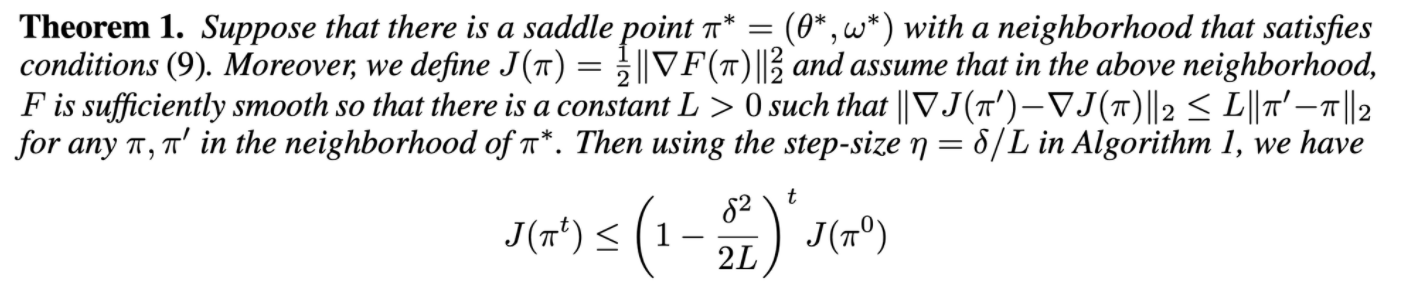
3.2. Practical Considerations
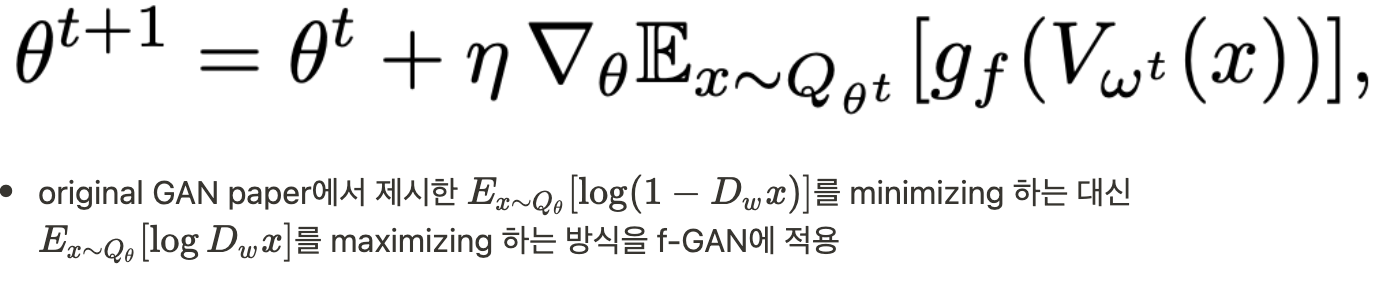
4. Experiments
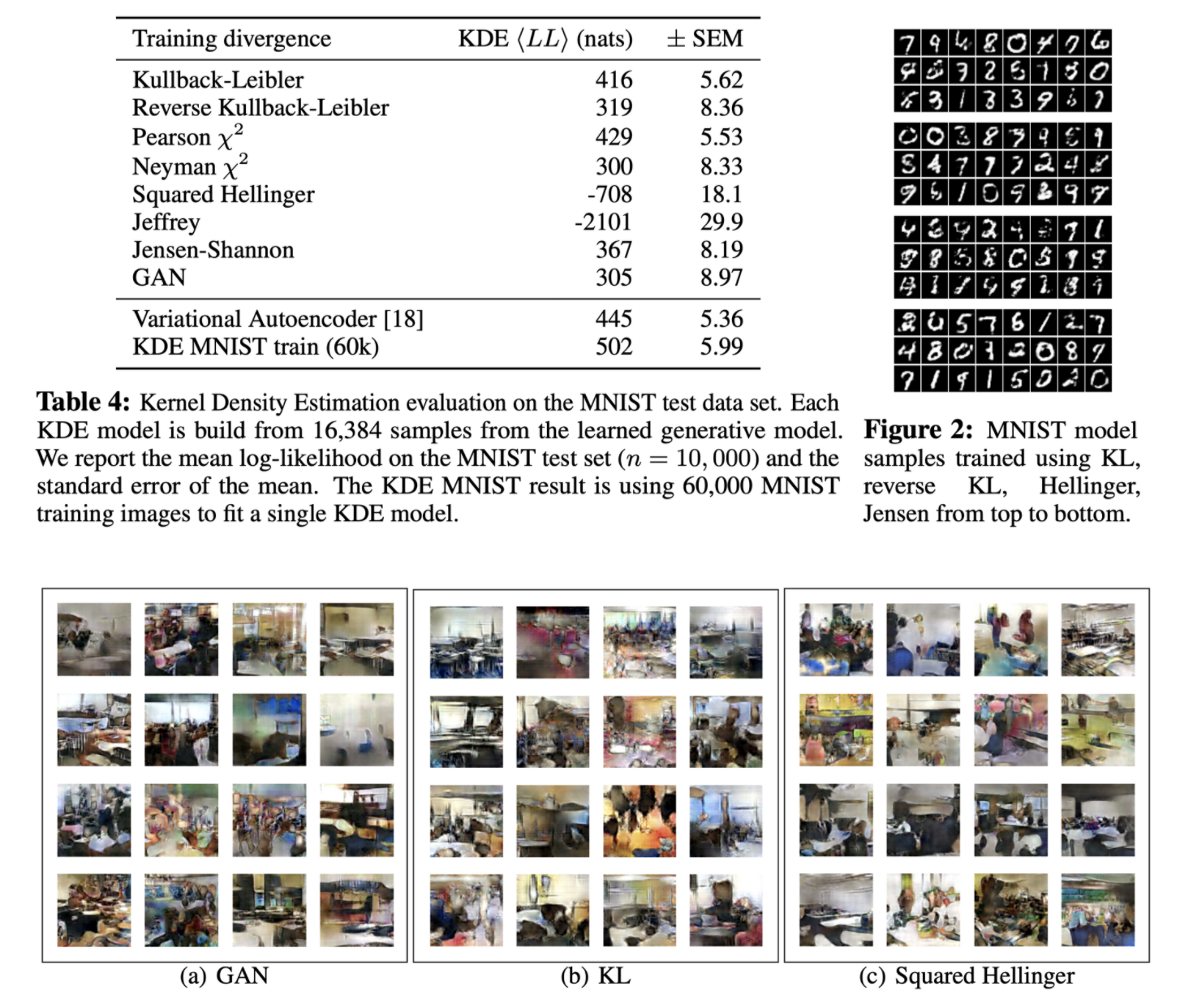
- GAN, KL, Squared Hellinger 등 다양한 divergence를 사용하였지만 생성결과에서 눈에 보이는 큰 차이가 없음
- 저자는 이를 실제 분포 P와 근사 분포 Q의 차이가 divergence 선정에 따른 Q 내부의 q의 차이보다 크기 때문에 생기는 상대적인 문제로 추측
후기 & 정리
- generative-adversarial approach가 variational divergence estimation approach의 special case임을 말하는 논문
- f-divergence family의 generator function, output activation을 모두 제시
- conjugate function, Jensen’s inequality, Fenchel conjuagte, duality 등 convex optimization에 대한 학습을 하느라 오랜 기간 읽었던 논문
- 선택한 divergence에 따라 의미 있게 다른 결과가 나오지 않았지만 분포 간 f-divergence에서 시작해서 generative adversarial approach의 expectation minimax수식에 도달하는 과정을 직접 전개해보며 많은 도움이 되었음
- 후에 convex optimization에 대한 학습을 따로 진행하고 다시 읽어보면 더 깊게 이해할 수 있을 것이라 생각함
Reference
[0] Sebastian Nowozin et al. (2016). "f-GAN: Training Generative Neural Samplers using Variational Divergence Minimization". https://arxiv.org/pdf/1606.00709.pdf
[1] https://greeksharifa.github.io/generative%20model/2019/03/19/f-GAN/
'AI > Deep Learning' 카테고리의 다른 글
| RoBERTa: A Robustly Optimized BERT Pretraining Approach (0) | 2022.06.01 |
|---|---|
| VQ-VAE: Neural Discrete Representation Learning (0) | 2022.04.14 |
| GAN: Generative Adversarial Nets (0) | 2022.03.28 |
| Font Generation with Missing Impression Labels (0) | 2022.03.23 |
| VAE: Auto-Encoding Variational Bayes (0) | 2022.02.26 |
Comments




