| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- userwidget
- 생성모델
- cv
- deep learning
- Diffusion
- motion matching
- 폰트생성
- CNN
- ddpm
- ue5.4
- Font Generation
- UE5
- 디퓨전모델
- WinAPI
- GAN
- 언리얼엔진
- Few-shot generation
- 오블완
- NLP
- 딥러닝
- WBP
- RNN
- Generative Model
- dl
- Unreal Engine
- 모션매칭
- animation retargeting
- BERT
- Stat110
- multimodal
Archives
- Today
- Total
Deeper Learning
VAE: Auto-Encoding Variational Bayes 본문
Diederik P. Kingma, Max Welling, Machine Learning Group Universiteit van Amsterdam. (2013)
Abstract
- intractable posterior, large dataset, continous latent variable 환경에서 directed probabilistic model의 추론, 학습을 어떻게 효율적으로 할 수 있을까?
- mild 한 미분 가능 조건하에 intractable case에서도 가능하며 large dataset을 다룰 수 있는 stochastic variational inference와 학습 알고리즘을 제시
- Contribution
- variational lower bound에 reparameterization을 적용하면 SGD로 최적화가 가능한 lower bound estimator를 만들 수 있음
- datapoint마다 continuous latent variable를 가지는 i.i.d dataset에서 논문에서 제시한 lower bound estimator를 사용하여 approximate inference model(NN으로 설정)을 intractable posterior에 fitting 성공
1. Introduction
- intractable posterior로의 근사에 대한 최적화는 Variational Bayesian(VB)를 통해 가능하다.
- 하지만 Mean-field approximation은 approximation posterior의 expectation의 analytic solution을 필요로 함 (수치로 표현 가능한 해, closed form)
- 하지만 일반적인 case에서 approximation posterior 또한 intractable
- variational lower bound의 reparameterization을 통해 lower bound에 대한 간단한 미분가능한 unbiased estimator를 만드는 과정을 논문에서 소개 예정
- 제시하는 Stochastic Gradient Variational Bayes(SGVB)는 연속적인 latent, parameters를 가지는 어떤 모델에서도 효율적인 posterior 근사를 하는데에 사용할 수 있으며, stochastic gradient ascent를 사용하여 최적화가 가능
- datapoint 마다 연속적인 latent variables, i.i.d dataset case를 위한 Auto-Encoding VB(AEVB) 알고리즘을 제시
- AEVB 알고리즘은 SGVB estimator를 사용하여 간단한 ancestral sampling을 사용하여 posterior 근사를 하는 recognition model이 최적화될 수 있도록 함 (ex. x를 샘플링하고 그에 따라 z를 샘플링)
- AEVB는 Markov Chain Monte Carlo(MCMC)와 같이 반복적인 과정이 없이 모델 파라미터를 학습
- recognition model로 neural net을 사용할 때 variational auto-encoder라고 이름 붙임
2. Method
- 이번 section은 연속적인 latent variable을 가진 directed graphical model에서 lower bound estimator를 도출하는 전략에 대해 설명
- 앞으로 설명할 common case 제약
- data point마다 latent variables를 가지는 i.i.d dataset
- maximum likelihood(ML) or maximum a posterior(MAP) inference를 parameters에 적용
- variational inferecne를 latent variable에 적용
- global parameter까지 variational inference를 사용하는 방식은 future work으로 제시

- 위 그림은 directed graphical model, 실선은 generative model pθ(z)pθ(x|z)을 뜻하며 점선은 intractable posterior pθ(z|x)에 대한 variational inference qϕ(z|x) 를 뜻함
- variational parameters ϕ 는 generative model parameters θ 와 함께 학습됨
- N개의 i.i.d 샘플 x로 구성된 데이터셋을 X={xi}Ni=1 이라고 하자
- 관측되지 않은 연속적인 랜덤 variable z가 어떤 랜덤 process를 거쳐 data가 생성된다고 가정하면 이 process는 2 step으로 구성되어 있다.
- zi가 어떤 prior distribution pθ∗(z)(prior)에서 샘플링
- xi가 어떤 conditional distribution pθ∗(x|z)(likelihood)에서 생성
- prior, likelihood의 PDF는 θ,z에 대해 거의 모든 지점에서 미분 가능
- 문제는 우리가 현재 true parameter θ∗, latent variable z(i)를 모른다는 것
- marginal, posterior probabilities에 대한 단순한 가정을 하지 않고 일반적인 알고리즘을 적용
- Intractability
- marginal likelihood pθ(x)=∫pθ(z)pθ(x|z)dz는 intractable
- posterior density pθ(z|x)=pθ(x|z)pθ(z)/pθ(x)는 intractable
- 복잡한 likelihood function pθ(x|z)에서 intractability는 자주 발생 (NN과 같은 복잡한 비선형 함수)
- large dataset
- batch optimization은 매우 느리기 때문에 minibatches를 사용
- Monte Carlo EM과 같은 샘플링 베이스 방식은 datapoint마다 오래 걸리는 sampling loop로 인해 사용이 어려움
- Intractability
- 위와 같은 시나리오를 위한 솔루션은 다음과 같다
- paremeter θ에 대한 효율적인 ML or MAP 근사 추정
- pθ(z|x) 에 대한 효율적인 근사 posterior 추정
- x의 marginal에 대한 효율적인 근사
- 위 문제를 해결하기 위해 recognition model qϕ(z|x)를 소개
- intractable posterior pθ(z|x)에 대한 근사
- mean-field variational inference와 다르게 closed-form으로 계산이 불가능하며 factorized 또한 필요 없음
- generative model parameter θ,ϕ는 동시에 학습
- qϕ(z|x)를 encoder, pθ(x|z)를 decoder, z를 code로 이름 붙임
2.2. The variational bound
- marginal likelihood는 datapoint의 marginal likelihood의 합
- logpθ(x(1),x(2),...,x(N))=ΣNi=1logpθ(x(i))
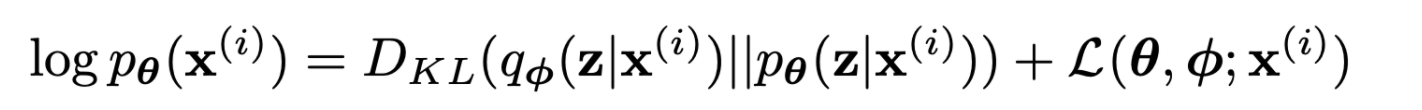
- first RHS term은 true posterior에 대한 근사의 KL divergence로 non-negative
- second RHS term은 lower bound라고 불림, lower bound를 다시 전개하면
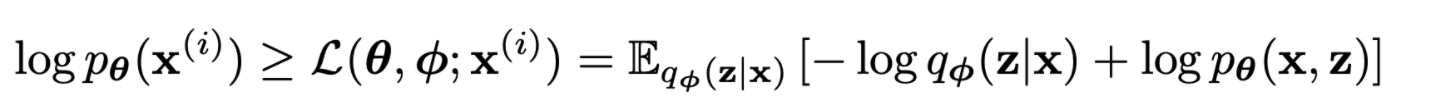

- lower bound를 ϕ,θ로 미분이 가능하기를 원함
- 하지만 ϕ에 대한 미분에 문제가 있는데 Monte Carlo gradient estimator에서 variance가 커서 실용적이지 않음. (https://andymiller.github.io/2016/12/19/elbo-gradient-estimators.html 참고)

2.3. The SGVB estimator and AEVB algorithm
- 이번 section은 lower bound의 practical estimator와 parameter에 대한 그 미분에 대해 소개
- posterior에 대한 근사 form을 qϕ(z|x)로 가정 (x conditioning이 없는 qϕ(z)에 대해서도 적용 가능)
- **2.4.**에서 소개할 reparameterization trick을 사용하여 random variable ˜z∼qϕ(z|x)를 역전파 가능한gϕ(ϵ,x),ϵ∼p(ϵ)으로 변형
- 이제 어떤 function f의 qϕ(z|x)에 대한 기댓값을 Monte Carlo 추정 가능

- 위의 방식을 (eq.2)에 적용하면 generic Stochastic Gradient Variational Bayes(SGVB) estimator ˜LA가 산출됨

- 보통 (eq.3)의 KL term은 (prior z와 VI로 근사한 posterior의 KL divergence) 수치계산이 가능한 분석가능해, 따라서 reconstruction error term만 sampling을 통한 estimation이 필요
- KL term을 근사한 posterior를 prior와 가깝도록 ϕ를 규제하는 것으로 해석하고 이를 (eq.3)에 적용하면 다음과 같은 식의 SGVB estimator ˜LB\tilde{L}^B가 산출됨

- N개의 data로 구성된 데이터셋 X, batch size가 M일 때 marginal likelihood lower bound estimator는 아래와 같음
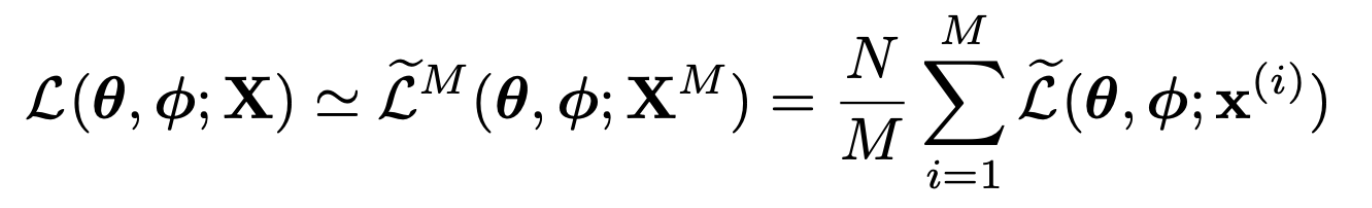
- ˜LB를 auto-encoder의 시각으로 보면 KL term은 regularizer, second term은 negative reconstruction error
2.4. The reparameterization trick
- 역전파를 가능하게 하기 위한 trick
- indepedent auxiliary variable ϵ를 사용하여 같은 분포이나 z의 parameter set에 대한 미분이 가능하도록 변경 (z=μ+σϵ)
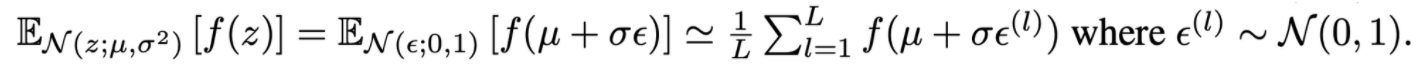
3. Example: Variational Auto-Encoder
- 이번 section에서는 neural network을 probabilistic encoder qϕ(z|x)에 사용하는 부분, AEVB 알고리즘이 ϕ,θ를 동시에 optimize 하는 방식에 대해 소개
- prior를 centered isotropic multivariate Gaussian로 정하면 pθ(z)=N(z;0,I)
- pθ(x|z)를 multivariate Gaussian or Bernoulli로 정함 (분포를 결정하는 parameter는 z를 input으로 하는 MLP에 의해 결정)
- intractable true posterior를 diagonal covariane를 가지는 Gaussian form으로 생각하면 variational approximation posterior를 diagonal covariance를 가지는 multivariate Gaussian로 정할 수 있음

- diagonal covariance인 두 Gaussian 분포의 KL divergence는 계산이 아래와 같이 간단해짐
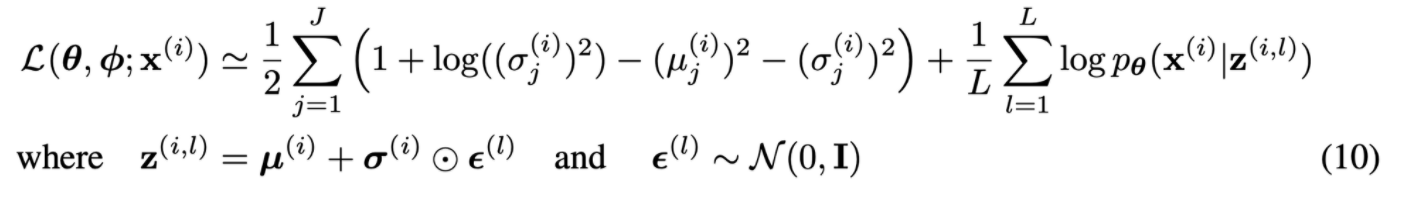
5. Experiments
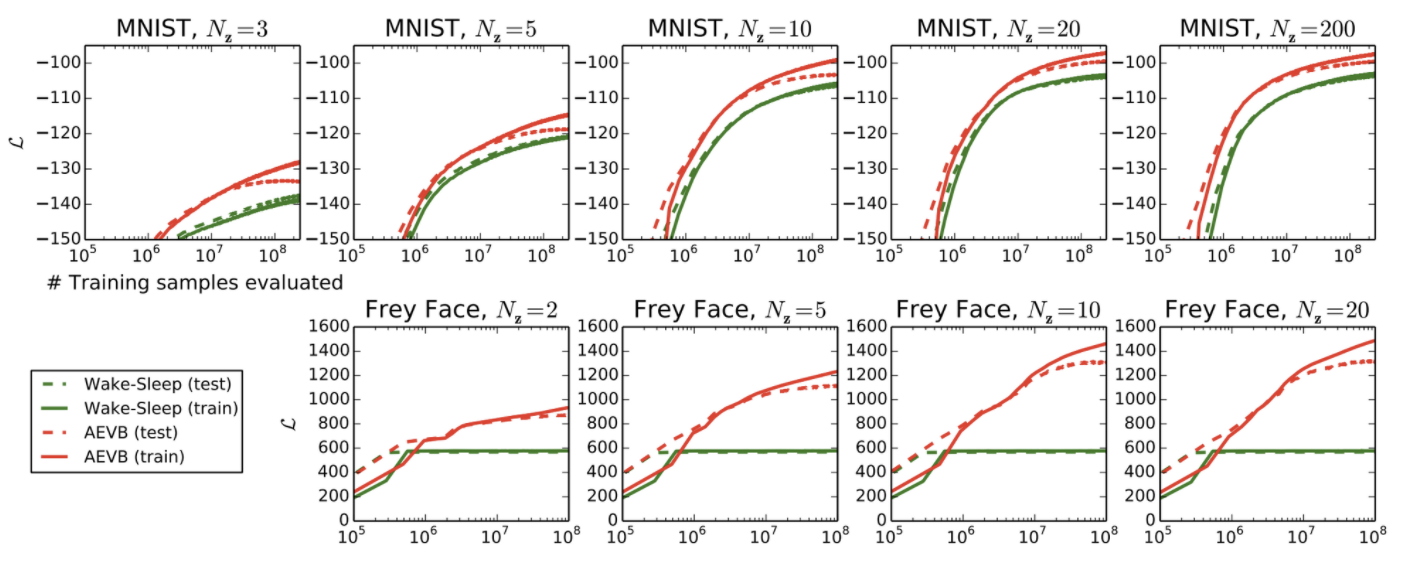
- wakeup sleep 알고리즘(Geoffrey E Hinton, 1995)과의 비교

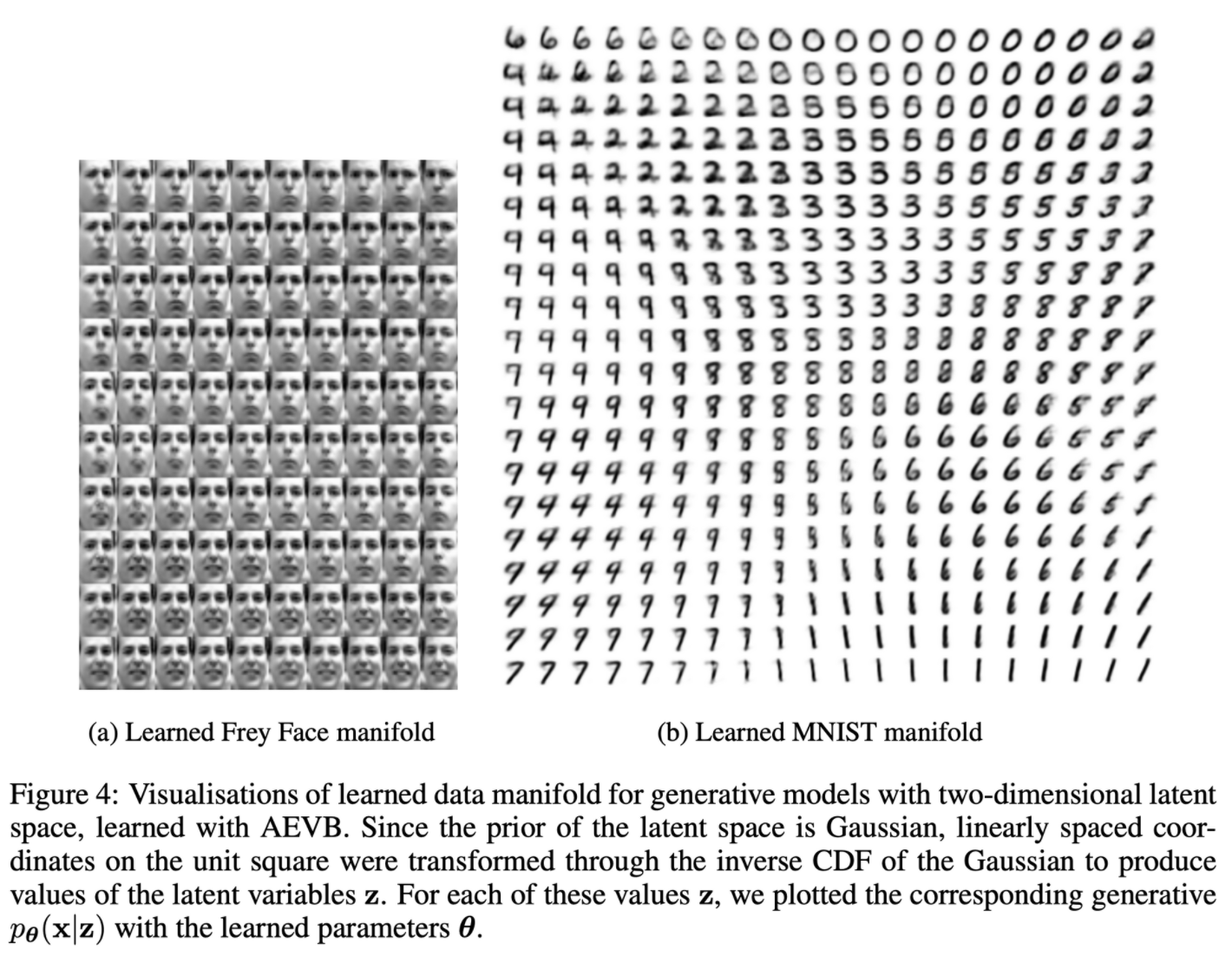
- manifold visualization
6. Conclusion
- 연속적인 latent variable로 효율적인 approximation inference가 가능하며 stochastic gradient method를 사용 가능한 variational lower bound의 novel estimator SGVB를 제시
- i.i.d dataset, datapoint마다 연속적인 latent variables 세팅에서 SGVB estimator를 사용하여 approximate inference model을 효율적으로 학습시키는 AEVB 알고리즘 제시
- Future work
- CNN을 사용한 VAE
- time-series model
- SGVB를 global parameter에 적용
- 복잡한 noise distribution을 학습하는 supervised model
후기 & 정리
- VAE를 제시한 원 논문을 읽어보고자 결심하고 나서 배경지식을 쌓기 위해 2주 정도 쉽게 정리한 글, 강의를 많이 보고 나서 읽은 논문
- ancestral sampling, wake-sleep algorithm 등 생소한 개념이 많아 쉽게 읽히지 않았던 논문
- 논문을 읽으며 많은 수학, 통계 개념을 찾아볼 수 있어서 좋았음
- VAE의 개념을 정리한 글과 강의는 많이 보았기 때문에 쉽게 요약하기보다 논문 그대로를 서술하려고 노력하였음
Reference
[0] Diederik P. Kingma et al.(2013). “Auto-Encoding Variational Bayes”. https://arxiv.org/pdf/1312.6114.pdf
[1] Geoffrey E Hinton. (1995). “The wake-sleep algorithm for unsupervised neural networks”. https://www.cs.toronto.edu/~hinton/csc2535/readings/ws.pdf
'AI > Deep Learning' 카테고리의 다른 글
| GAN: Generative Adversarial Nets (0) | 2022.03.28 |
|---|---|
| Font Generation with Missing Impression Labels (0) | 2022.03.23 |
| ConvMixer: Patches Are All You Need? (0) | 2022.02.21 |
| GANet: Glyph-Attention Network for Few-Shot Font Generation (0) | 2022.02.18 |
| AdaConv: Adaptive Convolutions for Structure-Aware Style Transfer (0) | 2022.02.15 |




