| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- CNN
- WBP
- dl
- userwidget
- 딥러닝
- WinAPI
- BERT
- Unreal Engine
- 모션매칭
- Generative Model
- animation retargeting
- RNN
- Font Generation
- Stat110
- Diffusion
- 언리얼엔진
- 생성모델
- NLP
- 폰트생성
- cv
- deep learning
- 오블완
- Few-shot generation
- ddpm
- motion matching
- 디퓨전모델
- GAN
- UE5
- ue5.4
- multimodal
Archives
- Today
- Total
Deeper Learning
GAN: Generative Adversarial Nets 본문
Ian J. Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, Yoshua Bengio, Universite de Montreal (2014.06)
Abstract
- 데이터 분포를 파악하는 generative model G와 sample이 training data에서 온 것인지 생성된 것인지 판별하는 discriminator D를 적대적인 프로세스로 동시에 학습하는 생성모델 프레임워크를 제시
- G는 D가 제대로 판별하지 못하도록 학습되는 minimax two-player game
- G와 D는 MLP로 구성하였으며 역전파를 통해 학습이 가능한 모델
- Markov chain 또는 approximate inference를 학습, 추론과정에서 사용하지 않으며 quantitative, qualitative evaluation으로 제시한 프레임워크의 가능성을 증명
1. Introduction
- 딥러닝은 분류 task에서 relu와 같은 piecewise linear units을 사용하여 gradient vanishing과 같은 문제를 완화시키고 성공적인 학습을 이룸
- 하지만 Deep generative model의 경우 MLE나 다른 접근법의 적용에서 마주치는 intractable probabilistic computations 근사에서 어려움이 있으며 piecewise linear units의 장점을 활용하기도 쉽지 않음
- 이러한 문제점을 피해갈 수 있는 생성모델 추정 방법론을 제시
- 제시한 적대적 네트워크 프레임워크에서 generative model은 model 분포와 data 분포를 판별하는 discriminator와 적대적인 관계를 가진다.
- 마치 generative model은 위조지폐범, discrminative model은 경찰과 같은 관계로 둘의 경쟁으로 generative model은 판별 불가능한 진짜 같은 sample을 생성하도록 학습된다.
- random noise를 input으로 sample을 생성하는 MLP로 구성된 generative model, sample을 판별하는 MLP로 구성된 discriminative model을 사용하는 case를 adversarial nets으로 명명
2. Related work
- explicitly probability distribution defining 대신 generative machine이 목표로 하는 분포로부터 sample을 뽑아내도록 학습하는 method가 존재
- 위 method의 경우 역전파로 학습이 가능하다는 장점이 있음
- denosing auto-encoders 그리고 이를 확장한 형태의 generative stochasitc network(GSN) framework은 모두 parameterized Markov chainn을 정의 (generative Markov chain의 1 step으로 machine의 parameter를 학습)
- 제시한 adversarial nets은 generation step에서 feedback loop가 필요없기 때문에 sampling에 Markov chain을 사용하지 않는다
- adversarial nets은 relu와 같은 piecewise linear units의 역전파의 성능 측면의 장점을 활용할 수 있으나 feedback loop 내의 unbounded activation으로 인한 문제가 존재
- 역전파로 학습하는 생성모델의 최신 연구는 VAE, stochasitc backpropagation 등이 있다
3. Adversarial nets
- generator의 분포 pg가 data x에 대한 분포를 학습하기 위해 input noise variables pz(z)의 prior를 정의한다
- data space로의 매핑: G(z;θg)에서 G는 parametes θg를 가지는 MLP로 구성되어있다
- D(x;θd)는 x가 pg가 아닌 data에서 나왔을 확률(scalar)이 output

- G와 D는 위와 같은 value function을 사용하여 학습된다

- 위 그림을 보면 1번 지점에서는 생성 결과가 좋지 않음에도 적은 graient가 발생하며 2번 지점에서는 생성 결과가 1번 지점보다 훨씬 좋음에도 불구하고 더 큰 gradient가 발생, 초기 학습이 더딘 문제를 해결하기 위해 log(1−D(G(z)))를 minimize하지 않고 log(D(G(z))를 maximize하는 방식을 사용

- 검정선: data 분포, 파랑선: discriminator decision, 초록선: generative distribution pg
- (b): discriminator가 학습, (c): Generator 학습, (d): 여러 스텝 이후 Nash equilibrium 도달
4. Theoredical Results
- G는 확률분포 pg를 직접 정의하는 것이 아닌 G가 만들어낸 samples G(z)가 특정 지표를 만족하도록 학습하면서 implicit하게 정의

- 위 알고리즘을 사용하면 충분한 capacity와 time이 주어진다면 pdata의 좋은 estimator로 수렴
4.1 Global Optimally of pg = pdata
- G가 fixed 상황에서, optimal discriminator D는 아래와 같다
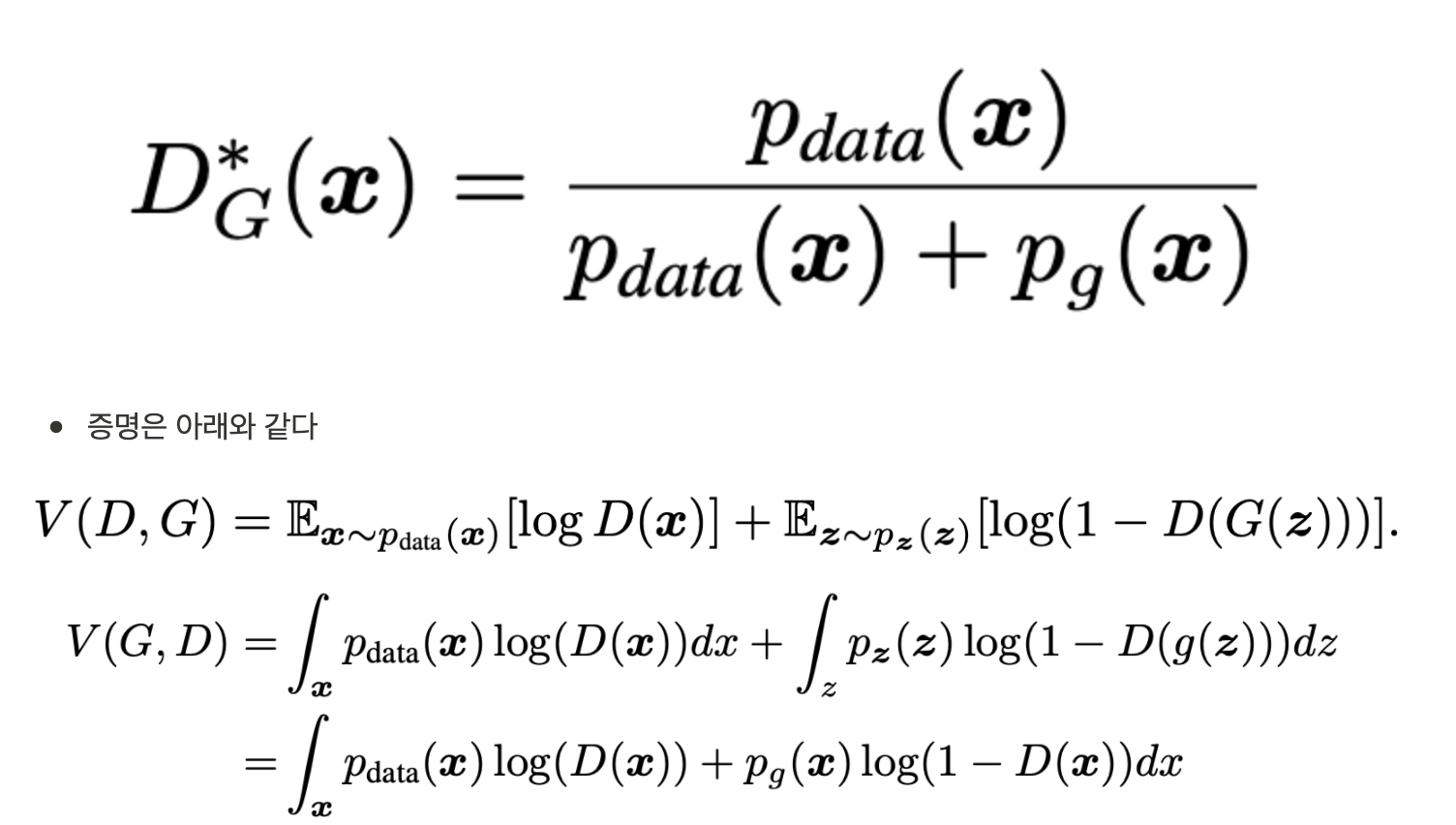
- 둘다 0이 아닌 실수 a,b에서 y=alog(y)+blog(1−y)는 aa+b에서 최댓값을 가짐
- D의 학습 목표는 조건부 확률 P(Y=y|x)를 추정하기 위한 maximizing log-likelihood로 해석할 수 있다. optimal D∗를 가정하고 다시 수식을 써보면 아래와 같다

- Theorem 1: C(G)의 global minimum은 오직 pg=pdata일 때 얻을 수 있으며 이때 C(G)의 값은 -log4
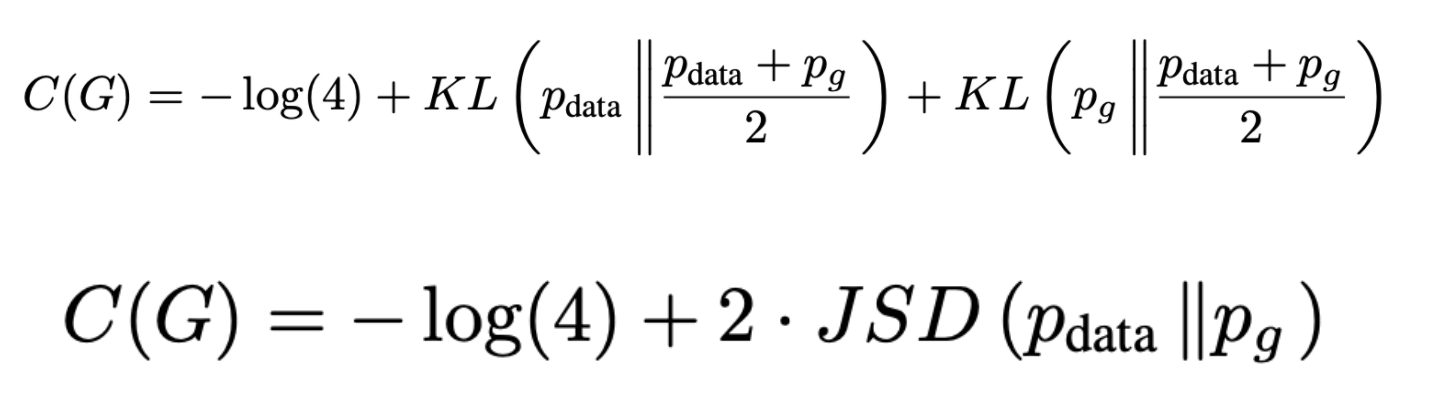
- 익히 알고있는 Kullback-Leibler Divergence 식을 이용하여 식을 전개해보면 위처럼 pdata,pg의 Jensen-Shannon divergence를 줄이는 것이 GAN의 목적함수임을 알 수 있다 (자세한 전개는 생략, KL식 대입이 전부인 간단한 과정)
- Jensen-Shannon divergence는 0이상의 값을 가지기 때문에 global minimum C(G)=−log(4)이며 이때 pg=pdata가 유일한 solution (생성모델이 data의 분포를 완벽하게 모방)
4.2 Convergence of Algorithm 1
- 지금까지 설명한 세팅으로 (G,D,V(G,D)) 학습을 진행할 경우 pg가 pdata로 적은 update로도 수렴한다
- 증명의 골자는 아래와 같은 목적함수가 θg에 대해서 convex하다는 것

- 실제로는 pg가 아닌 parameter set θg를 optimize하기 때문에 parameter space에 critical point가 여럿 존재하지만 MLP의 성능은 뛰어났다 (MLP는 이론적 보장이 부족하더라도 reasonble model)
5. Experiments

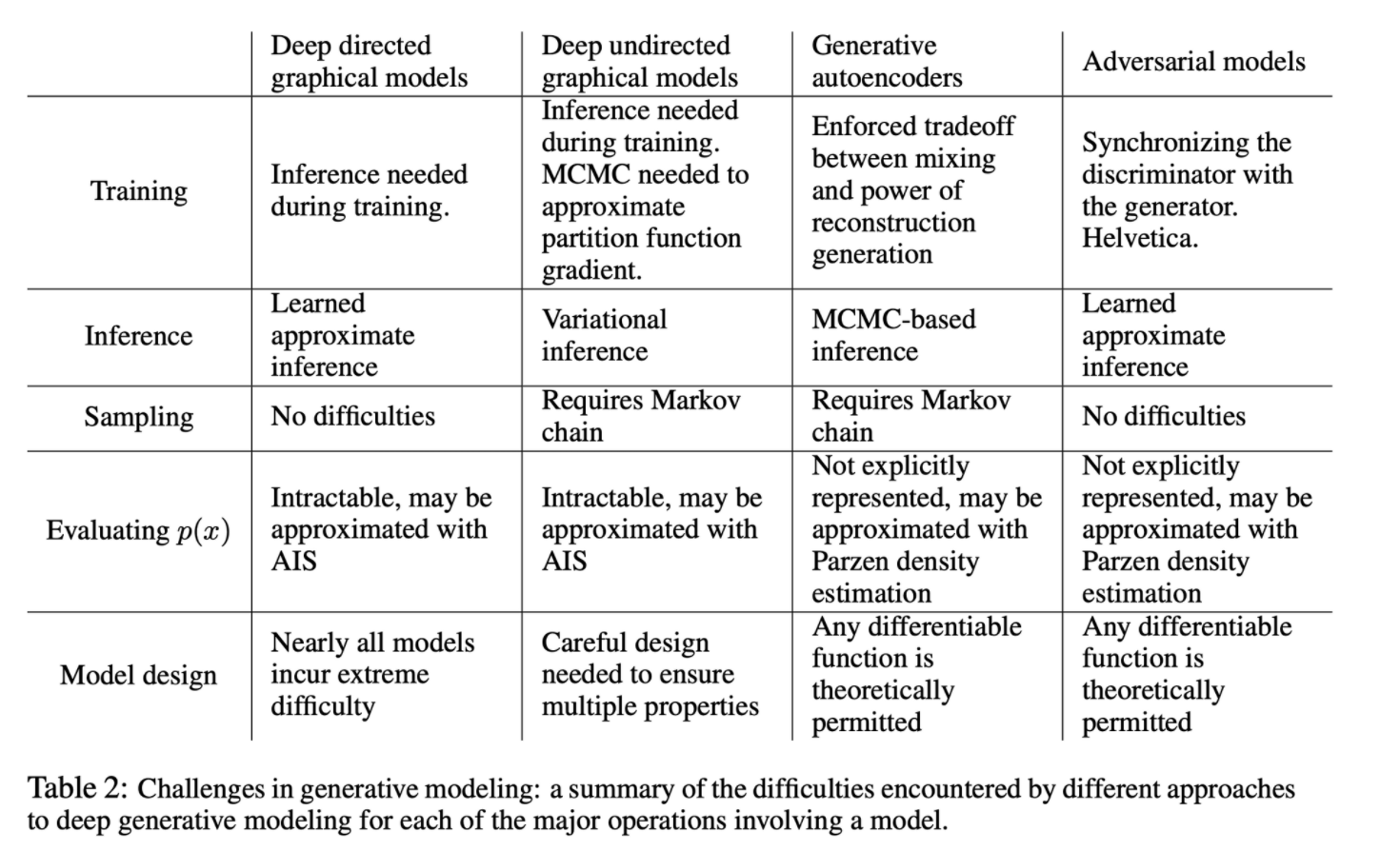
6. Advantages and disadvantages
장점
- 학습 중 추론이 필요없음
- Markov chain이 필요 없음
- 결과가 sharp
단점
- pg(x)의 explicit representation의 부재
- 학습이 어렵다
7. Conclusions and future work
Future work
- Conditional generative model
- generator의 학습이 끝난 후 x → z를 추정하는 auxiliary network 학습을 통한 approximate inference 학습
- MP-DBM의 stochastic extension
- Semi-superviesed learning (discriminator)
- Efficiency improvements
정리 & 후기
- 적대적인 프로세스 기반 생성모델인 GAN을 제시
- 데이터 분포와 생성 데이터 분포의 Jensen-Shannon divergence를 줄이도록 학습
- 이전에 보았던 논문이라 논문의 흐름만 가볍게 기술
Reference
[0] Ian J. Goodfellow at al. (2014). "Generative Adversarial nets". https://arxiv.org/abs/1406.2661
'AI > Deep Learning' 카테고리의 다른 글
| VQ-VAE: Neural Discrete Representation Learning (0) | 2022.04.14 |
|---|---|
| f-GAN: Training Generative Neural Samplers using Variational Divergence Minimization (0) | 2022.04.07 |
| Font Generation with Missing Impression Labels (0) | 2022.03.23 |
| VAE: Auto-Encoding Variational Bayes (0) | 2022.02.26 |
| ConvMixer: Patches Are All You Need? (0) | 2022.02.21 |




