| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- CNN
- BERT
- 생성모델
- Diffusion
- 오블완
- RNN
- Font Generation
- userwidget
- ue5.4
- 모션매칭
- 폰트생성
- NLP
- 딥러닝
- 언리얼엔진
- ddpm
- motion matching
- deep learning
- GAN
- dl
- Unreal Engine
- Few-shot generation
- 디퓨전모델
- UE5
- WinAPI
- cv
- Generative Model
- multimodal
- Stat110
- WBP
- animation retargeting
- Today
- Total
목록분류 전체보기 (220)
Deeper Learning
망각성질(무기억성, memoryless property) 이산확률분포는 기하분포, 연속확률분포에서는 지수분포가 유일 확률변수 $X$가 모두 양수이며, 연속적이고 무기억성을 가진다면 그 확률변수가 따르는 확률분포는 지수분포가 유일하다. proof) $X$의 cdf를 $F(X)$라고 하자 $$ G(X) = P(X>x) = 1 - F(x)\\G(s+t) = G(s)G(t)\space memoryless\\G(kt) = G(t)^k\\ G(1x) = G(1)^x = e^{xlnG(1)} = e^{-\lambda x} = 1-F(x) $$ 기대수명 기대수명을 구하는 방법은? 어느 날 태어난 아기들을 모두 관찰하고 특정 연도에 죽은 사람의 나이를 측정 문제는 아직 죽지 않은 사람들의 데이터가 무시됨 → 중도절단 데..
Exponential Distribution(지수분포) $X \sim Expo(\lambda)$. pdf $f_X(x) = \lambda e^{-\lambda x}$, (x >0), otherwise 0 cdf $$ F_X(x) = \int_0^x \lambda e^{-\lambda t} dt = 1-e^{-\lambda t} $$ 성질 $Y = \lambda X$이면, $Y \sim Expo(1)$. 증명은 아래와 같다 $$ P(Y \le y) = P( X \le \frac y\lambda) = 1-e^{-\lambda\frac{y}{\lambda}} = 1-e^{-y} = cdf \space of \space Expo(1) $$ Expected value (부분적분 사용) $$ E(Y) = \int_..
 [Statistics 110] Lecture 15: Midterm Review
[Statistics 110] Lecture 15: Midterm Review
Coupon Collector 뽑기 상품에서 같은 확률로 등장하는 n개 종류의 장난감이 있다. 이를 모두 수집하기 위해 뽑기를 평균 몇 번 해야할까? $T_j$를 j 번째 장난감을 얻기까지의 시도 횟수라고 하자 $T =T_1+T_2+...+T_n$. $T_1$은 무엇이든 뽑으면 바로 성공이기 때문에 1이고, $T_2$는 이제 성공확률이 n/n(n-1)인 시행이 되어 기하분포로 표현이 가능 $T_2-1 \sim Geom(\frac {n-1}{n})$. 일반화한 식은 $$ T_j -1 \sim Geom(\frac{n-(j-1)}{n}) \\ E(T) = E(T_1)+...+E(T_n) = 1+\frac{n}{n-1} + ... + \frac n1 \\ =n(1+\frac 12 + ... + \frac 1n)..
 [Statistics 110] Lecture 14: Location, Scale, and LOTUS
[Statistics 110] Lecture 14: Location, Scale, and LOTUS
표준정규분포 표준정규분포에서 기함수의 성질을 이용하면 $E(X) =0, E(X^2) = 1 , E(X^3) = 0$. 일반정규분포 $X \sim \mu + \sigma Z$ 라고 하면 $X \sim N(\mu, \sigma^2)$ 을 따른다 기댓값은 선형성에 의해 $E(X) = E(\mu) + \sigma(E(Z)) = \mu$. 분산의 성질 $$ Var(X) = E((X-E(X))^2) = E(X^2) - (E(X))^2 \\Var(X+c) = Var(X)\\Var(cX) = c^2Var(X)\\Var(X+Y) \ne Var(X) + Var(Y) $$ 일반정규분포의 분산 $$ Var(X) = Var(\mu+\sigma Z) = Var(\sigma Z) = \sigma^2Var(Z) = \sigma^2 ..
 [Statistics 110] Lecture 13: Normal Distribution
[Statistics 110] Lecture 13: Normal Distribution
Normal Distribution(정규분포) Central Limit Theorem(중심극한정리) 적당히 많은 수의 i.i.d 확률변수를 더하면 더한 평균값의 분포는 정규분포에 수렴한다 대칭인 종모양의 pdf 평균이 0이고 분산이 1이면 표준정규분포 $Z \sim N(0,1^2)$. PDF $$ f(z) = ce^{-z^2/2} $$ c는 normalize constant로 적분을 통해 c값을 구해보자 $$ \int_{-\inf}^{\inf} e^{-z^2/2}dz $$ closed-form으로 적분식 풀이가 불가능 $$ \int_{-\inf}^{\inf} e^{-x^2/2}dx\int_{-\inf}^{\inf} e^{-y^2/2}dy \\=\int_{-\inf}^{\inf}\int_{-\inf}^{\..
 SGCE-Font: Skeleton Guided Channel Expansion for Chinese Font Generation
SGCE-Font: Skeleton Guided Channel Expansion for Chinese Font Generation
Jie Zhou, Yefei Wang, Yiyang Yuan, Qing Huang, Jinshan Zeng (2022.11) Abstract 효과적인 가이드 정보가 없어 GAN-based 모델이 mode collapse 문제를 겪고 있음 본 연구는 skeleton guided channel expansion(이하 SGCE) 모듈로 skeleton 정보를 generator에게 channel expansion 방식으로 주어 local, global structure를 파악하게 하는 새로운 guidance 방식을 제시 SGCE 모듈을 통해 mode collapse 문제가 완화되었으며 실험을 통해 이를 보임 4개의 metrics에서 SOTA를 달성 다른 중국어 폰트 생성 모델에도 plug-and-play 모듈로..
 [Statistics 110] Lecture 12: Discrete vs. Continuous, the Uniform
[Statistics 110] Lecture 12: Discrete vs. Continuous, the Uniform
Probability Density Function(PDF) 정의 확률변수 $X$가 모든 a,b에 대해 $P(a\le X \le b) = \int_{a}^bf(x)dx$ 를 만족시키면, $X$는 확률밀도함수(PDF) $f_X(x)$를 가짐 a=b라면 적분값은 0 = 특정 값을 가질 확률은 0 pmf와 마찬가지로 음수가 아니며, 모든 구간에 대해 적분하면 1이 되어야 함 Density의 의미 CDF와 PDF의 관계 $$ F_X(x) = P(X\le x) = \int_{-\infin}^{x}f(t)dt $$ $$ pdf \space f_X(x) = cdf \space F'(x) $$ 기댓값 $$ E(X) = \int_{-\infin}^{\infin}xf_X(x)dx $$ 분산, 표준편차 $$ Var(x) =..
 [Statistics 110] Lecture 11: The Poisson distribution
[Statistics 110] Lecture 11: The Poisson distribution
확률변수와 확률분포의 혼동 확률변수 X, 확률변수 Y를 합하는 것은 확률변수 X가 따르는 확률분포와 Y가 따르는 확률분포를 합하는 것과 다름 X,Y가 이산확률변수라고 하면 $$ P(X+Y=k) \ne P(X=k) + P(Y=k) $$ 확률변수 $X+Y$의 pmf는 새로 찾아야 함 확률변수가 집(랜덤)이라면 확률분포는 집의 설계도(문이 빨간색일 확률, 문이 파란색일 확률) Poisson Distribution(포아송분포) $X \sim Pois(\lambda)$ PMF $$ P(X=k) = e^{-\lambda}\frac{\lambda^k}{k!}, k=\{0,1,...,\} $$ Expected value $$ E(X) = e^{-\lambda}\sum_{k=0}^{\infin}k\frac{\lambda..
 [Statistics 110] Lecture 10: Expectation Continued
[Statistics 110] Lecture 10: Expectation Continued
Linearity Proof. $T=X+Y \rightarrow E(T) = E(X)+E(Y)$ 기댓값을 구하는 2가지 방식을 다시보면 가중치 없이 모두 더하기 같은 그룹으로 묶어 가중치 주기 $$ E(T) = \sum_ttP(X=t) $$ 위 식은 그룹으로 묶어 가중치를 주는 형태이고 위 그림(pebble world)에서 각 조약돌을 모두 더하는 방식은 가중치 없이 모두 더하는 기댓값 계산법 각 조약돌을 $s$라고 하고 등식을 세워보면 (P(s)는 조약돌의 질량) $$ E(T) = \sum_ttP(X=t) = \sum_sX(s)P(\{s\}) $$ 위 등식을 가지고 discrete case에서 Expected values의 Linearity 증명을 이어간다 $$ E(T) = \sum_S(X+Y)(s)P..
 [Statistics 110] Lecture 9: Expectation, Indicator Random Variables, Linearity
[Statistics 110] Lecture 9: Expectation, Indicator Random Variables, Linearity
Average, Expected values, Mean은 아래에서 모두 같은 의미로 사용 CDF $F(x) = P(X\le x)$ cdf에서 pmf를 구하고 싶으면 값이 뛰는 수치를 계산 cdf $F$를 사용하여 $P(1
Binomial Distribution Story n번의 독립적인 Bern(p) 시행에서 성공 횟수 Sum of Indicator Random Variables $X = X_1+X_2+...+X_n$ $X_j$는 trial이 성공하면 1, 그렇지 않으면 0으로 2개의 값을 가질 수 있음 $X_j$는 independent identically distributed(i.i.d) 확률분포와 확률변수의 구분 확률변수는 수학적으로 함수 $X_j$는 시행이 성공하면 1, 아니면 0 확률분포는 $X$가 어떻게 다르게 행동할지에 대한 확률을 말함 같은 분포를 가진 확률변수가 여럿 존재 가능 i.i.d condition에서 확률변수들은 같은 분포를 가지지만 다른 값이 될 수 있음 PMF $X$가 특정값을 가질 확률을 수..
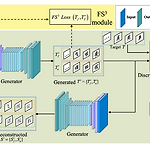 StrokeGAN+: Few-Shot Semi-Supervised Chinese Font Generation with Stroke Encoding
StrokeGAN+: Few-Shot Semi-Supervised Chinese Font Generation with Stroke Encoding
Jinshan Zeng, Yefei Wang, Qi Chen, Yunxin Liu, Mingwen Wang, and Yuan Yao, (2022.11) Abstract 현재 중국어 폰트 생성의 주류 방식은 GAN 기반 모델, 하지만 GAN 기반 모델은 mode collapse 문제를 겪고 있음 이 문제를 해결하기 위해 one-bit stroke encoding과 few-shot semi-supervised scheme으로 local, global structure 정보를 찾아내는 방식을 제시 해당 아이디어를 기반으로 본 논문은 stroke encoding과 few-shot semi-supervised scheme을 CycleGAN과 결합하여 mode collapse 문제를 완화한 StrokeGAN+를 제..
 Zero-Shot Text-to-Image Generation
Zero-Shot Text-to-Image Generation
Aditya Ramesh, Mikhail Pavlov, Gabriel Goh, Scott Gray, Chelsea Voss, Alec Radford, Mark Chen, Ilya Sutskever (2021.02) Abstract Text-to-Image(이하 TTI) generation은 고정된 데이터셋을 학습하기 위한 더 좋은 모델링 가정을 찾는 방향으로 연구가 집중되었음 이러한 가정은 복잡한 아키텍처, auxiliary loss 그리고 object part labels, segmentation mask와 같은 side information을 수반 하지만 저자는 text와 image token을 하나의 stream으로 처리하여 transformer-based 아키텍처로 autoregressive하게 ..
 [Statistics 110] Lecture 7: Gambler's Ruin and Random Variables
[Statistics 110] Lecture 7: Gambler's Ruin and Random Variables
Gambler’s Ruin 두 도박사 A, B가 1달러를 걸고 게임을 반복. A가 이길 확률은 $p$, B가 이길 확률은 $1-p$. B가 파산하여 A확률 $p_i = P(A \space wins \space game|A \space starts \space at \space \$i)$로 정의 $p_i = pp_{i+1} + qp_{i=1}$ (1 ≤ i ≤ N-1) 이전 스텝에서 이겨서 현재 위치에 도달했거나 다음 스텝에서 져서 현재 위치에 도달했기 때문에 위와 같이 표현이 가능 [계차방정식(difference equation)] A가 이길확률이 0.49라면 N이 100일때 0.02 확률로 승리 확률변수 확률변수는 Sample space → 실수 공간을 매핑해주는 함수 확률변수 x가 베르누이 분포를 따..
 [Statistics 110] Lecture 6: Monty Hall, Simpson's Paradox
[Statistics 110] Lecture 6: Monty Hall, Simpson's Paradox
Monty Hall 하나의 문 뒤에는 자동차, 2개의 문 뒤에는 염소가 있다. 참가자가 하나의 문을 고르고 사회자는 나머지 2개의 문 중에서 염소가 있는 문을 연다. 참가자는 그 뒤 선택할 문을 바꿀 기회가 주어지는데 문을 바꾸는 것이 자동차를 선택할 확률을 높여줄까? 수형도 참가자가 1번 문을 골랐다고 가정 자동차가 1,2,3번 문 뒤에 있을 확률은 각 1/3 사회자는 참가자가 고르지 않은 2 or 3번 문을 여는데, 여기에서 위 수형도를 보면 자동차가 1번 문 뒤에 있다면 사회자는 2,3 번 문을 동일한 확률로 열지만 자동차가 3번 문 뒤에 있다면 사회자는 2번 문 밖에 열 수 없다 “사회자가 2번문을 열었다”라는 조건 하에 각 분기의 확률을 보면 참가자가 1번 문 고름 → 자동차가 1번 문 뒤에 있..
 [Statistics 110] Lecture 5: Conditioning Continued, Law of Total Probability
[Statistics 110] Lecture 5: Conditioning Continued, Law of Total Probability
Law of Total Probability 문제를 disjoint인 다른 사건들로 분할하여 푸는 방식 예제) 인구의 1%가 걸리는 병이 있는데 이 병에 걸리는 사건이 $D$, 검사 결과가 양성인 사건이 $T$ 라고 할 때 검사 결과가 양성일 때, 실제로 병에 걸렸을 확률은? ($P(D|T)$) 조건부 독립 사건 A, 사건 B가 사건 C가 발생하였을 때 독립인 상황 Reference [0] https://www.youtube.com/playlist?list=PL2SOU6wwxB0uwwH80KTQ6ht66KWxbzTIo Statistics 110: Probability Statistics 110 (Probability) has been taught at Harvard University by Joe Bli..
 [Statistics 110] Lecture 4: Conditional Probability
[Statistics 110] Lecture 4: Conditional Probability
독립 독립이란? 위 식이 성립하면 독립 두 사건은 서로 영향을 끼치지 않음 서로소(disjoint)와 독립을 혼동하는 경우가 많음 서로소: 사건 A,B가 disjoint면 A가 발생할 때 B는 발생하지 않음 (배반사건, 독립 X) 독립: 사건 A, B가 독립이면 A의 발생은 B의 발생과 관련 없음 Conditional Probability(조건부 확률) Pebble World 관점 총 9개의 조약돌이 있는 sample space가 있다고 가정하자 위 조건부 확률 식은 사건 A(빨간색)가 일어났을 때의 사건 B(초록색)의 확률과 같다 이를 조약돌로 표현하면 사건 A,B에 공통으로 해당되는 조약돌 2개의 비중과 같다 사건 A가 일어났기 때문에 전체 world를 빨간 영역으로 줄이면 2/3이라는 답이 나온다 ..
 [Statistics 110] Lecture 3: Birthday Problem, Properties of Probability
[Statistics 110] Lecture 3: Birthday Problem, Properties of Probability
Birthday Problem $k$ 명의 사람이 있을 때 2명의 생일이 같을 확률을 구하라 2월 29일 제외 출생 계절성 고려하지 않음 (매일 같은 확률로 출생) 1 - P(k명의 생일이 모두 다른 경우) = P(2명 이상의 생일이 같을 확률) P(k명의 생일이 모두 다른 경우) = (365일을 중복없이[비복원추출] k명이 뽑을 확률) $$ \frac{365 \times 364 \times ... \times (365 - k + 1)}{365^k} $$ k = 23명일 때 50.7%, 50명일 때 97% 많은 우연이 하나도 발생하지 않는 상태가 가장 우연한 상태 (생일이 겹치는 2명의 조합의 수 253개 짝이 하나도 발생하지 않음) Non-naive Probability 확률 공리 (저번 강의에서 소개..
 [Statistics 110] Lecture 2: Story Proofs, Axioms of Probability
[Statistics 110] Lecture 2: Story Proofs, Axioms of Probability
순서 상관 있음, 복원추출 경우의 수 문제: n개의 가능한 결과를 가지는 실험을 k번 복원추출하는 경우의 수 (순서 상관 있음) n개의 상자에 k개의 구슬에 넣는다고 생각하자 (구슬을 넣는 행위를 추출로 생각, 주머니에서 1번 상자가 나왔다 == 1번 상자에 구슬 하나 넣기) 복원추출이므로 하나의 상자에 구슬이 여러개 들어갈 수 있음 (하나의 상자가 여러번 선택받을 수 있음) 이제 문제는 가지고있는 k개의 구슬을 어떻게 n개의 상자에 분배하느냐와 동일 이제 문제는 k+n-1의 자리에 k개의 구슬과 n-1개의 선을 배치하는 문제와 같음 Story Proof 1번 예시는 n명중 k명을 뽑는것은 n명 중 k명을 제외한 n-k명을 뽑는것과 동일하기 때문으로 해석가능 2번 예시는 n명의 축구선수 중 k명을 국가대..
 [Statistics 110] Lecture 1: Probability and Counting
[Statistics 110] Lecture 1: Probability and Counting
Statistics 110 복습하며 중심 내용 정리 확률 용어 Sample space: 발생 가능한 모든 실험의 결과의 집합 Event: Sample space의 부분집합 확률의 Naive한 정의 $$ P(A) = \frac{\#favorable \space outcomes}{\#possible\space outcomes} $$ 유한한 표본 공간에서 정의가 가능 모든 결과의 발생 확률을 같다고 가정함 어떤 외계 행성에 외계인이 있을 확률: 1/2 (있거나 없거나) Counting Principle 곱의 법칙(Multiplication Rule): $n_1,...,n_r$ 개의 가능한 결과가 있는 실험을 $r$번 하면 가능한 모든 경우의 수는 $n_1 \times ... \times n_r$개 예시로 A,..
 MLE(Maximum Likelihood Estimation), MAP(Maximum A Posterior)
MLE(Maximum Likelihood Estimation), MAP(Maximum A Posterior)
https://dlaiml.tistory.com/entry/Bayes-theorem Bayes' theorem 농어와 연어를 분류하는 문제 생선의 길이를 기준으로 농어, 연어를 분류 길이를 $x$, 물고기의 종류를 $w$ 라고 하자 물고기가 농어면 $w = w_1$, 연어면 $w = w_2$로 정의 Prior 사전확률인 Prior는 사전 dlaiml.tistory.com (Bayes theroem 포스팅에 이어서) Introduction 물고기의 길이 $x$, 물고기의 무게 $k$, 물고기의 길이로 물고기의 무게를 예측하는 회귀 문제를 예시로 들겠다. 필요로 하는것은 모든 $x$에 대해서 모든 $k$를 아는 함수 $k=g(x)$ (물고기의 길이에 따른 무게의 확률 밀도 함수) 이 함수를 parameter..
 Bayes' theorem
Bayes' theorem
농어와 연어를 분류하는 문제 생선의 길이를 기준으로 농어, 연어를 분류 길이를 $x$, 물고기의 종류를 $w$ 라고 하자 물고기가 농어면 $w = w_1$, 연어면 $w = w_2$로 정의 Prior 사전확률인 Prior는 사전지식을 반영 연어가 농어보다 3배 많다면 $P(w_1) = 0.25,P(w_2)=0.75$ 전체 사건 확률의 합은 항상 1이 되어야 함 Posterior 모든 $x$에 대해 $P(w_1|x), P(w_2|x)$ 값을 알면 두 값의 비교를 통해 쉽게 분류가 가능하다 즉, 길이 $x$가 주어졌을 때 두 클래스 $w_1, w_2$에 속할 확률을 알게되면 분류 문제를 해결한 것 이 확률 $P(w_i|x)$를 Posterior라고 함 Likelihood 확률밀도 $P(x|w_i)$는 물고기..
 CLIP: Learning Transferable Visual Models From Natural Language Supervision
CLIP: Learning Transferable Visual Models From Natural Language Supervision
Alec Radford, Jong Wook Kim , Chris Hallacy, Aditya Ramesh, Gabriel Goh, Sandhini Agarwal, Girish Sastry, Amanda Askell, Pamela Mishkin, Jack Clark, Gretchen Krueger, Ilya Sutskever, (2021.02) Abstract SOTA 컴퓨터 비전 시스템은 정해진 object의 카테고리를 예측하도록 학습하는 것 지도학습 방식은 라벨링된 데이터를 요구하기 때문에 일반화, 활용성에 제약이 존재 raw text-image pair 데이터를 학습하면 지도학습에서 더 많은 소스를 활용할 수 있음 raw text-image pair 데이터로 이미지 representation 학습을 ..
 Few-Shot Unsupervised Image-to-Image Translation
Few-Shot Unsupervised Image-to-Image Translation
Ming-Yu Liu, Xun Huang, Arun Mallya, Tero Karras, Timo Aila, Jaakko Lehtinen, Jan Kautz, [NVIDIA, Cornell University, Aalto University] (2019.05) Abstract Unsupervised image-to-image(i2i)는 여러 class 간 매핑을 학습하는 방법 최근 방법론들은 좋은 성과를 보였으나 학습과정에서 많은 수의 소스, 타깃 이미지를 필요로 하는 문제가 존재 인간은 매우 적은 수의 이미지로도 object를 잘 파악하는데에서 영감을 받아 few-shot 연구를 진행 저자는 새로운 모델 아키텍처, adversarial 학습 scheme을 함께 사용하여 few-shot generatio..
 Gram-Schmidt Process & QR Decomposition
Gram-Schmidt Process & QR Decomposition
Gilbert Strang의 MIT 18.06SC Linear Algebra 완강 후 딥러닝 논문 스터디, 개인 학습 중 다시 마주한 선형 대수 개념 정리 목적 Gram-schmidt Process linear independent column vectors를 직교화 해주는 방법론, orthogonal basis를 찾는 과정 Idea 선형독립인 두 벡터 $v_1, v_2$ 를 직교하는 두 벡터 $u_1, u_2$ 로 만들기 위해서는 우선 하나의 벡터 $v_1$ 을 $u_1$ 으로 두고 $v_2$ 를 $u_1$ 이 span하는 line에 정사영내린 $proj_{u_1}v_2$ 를 구하고 이를 $v_2$ 에서 빼주면 $u_1$ 과 직교하는 벡터 $u_2$ 를 얻을 수 있다. Process linear ind..
 FontTransformer: Few-shot High-resolution Chinese Glyph Image Synthesis via Stacked Transformer
FontTransformer: Few-shot High-resolution Chinese Glyph Image Synthesis via Stacked Transformer
Yitian Liu, Zhouhui Lian, [Wangxuan Institute of Computer Technology, Peking University, Beijing, China] (2022.10.13) Abstract 적은 데이터로 고품질의 중국어 폰트를 생성해내는 것은 어려운 일이며 현존하는 few-shot 폰트 생성 방식은 low-resolution의 획이 끊기는 폰트를 만드는데 그쳤다 이러한 문제를 해결하기 위해 본 논문은 고품질의 few-shot 생성이 가능한 FontTransformer를 제시 key idea는 prediction error가 쌓이는 것을 피하기 위한 parallel Transformer, 생성된 획의 퀄리티를 높이기 위한 serial Transformer의 사용 실제 ..
 GraphCodeBERT: Pre-training Code Representations with Data Flow
GraphCodeBERT: Pre-training Code Representations with Data Flow
Daya Guo, Shuo Ren, Shuai Lu, Zhangyin Feng, Duyu Tang, Shujie Liu, Long Zhou, Nan Duan, Alexey Svyatkovskiy, Shengyu Fu, Michele Tufano, Shao Kun Deng, Colin Clement, Dawn Drain, Neel Sundaresan, Jian Yin, Daxin Jiang and Ming Zhou [School of Computer Science and Engineering, Sun Yat-sen University, Beihang University, Peking University, Harbin Institute of Technology, Microsoft Research Asia, ..
 CodeBERT:A Pre-Trained Model for Programming and Natural Languages
CodeBERT:A Pre-Trained Model for Programming and Natural Languages
Zhangyin Feng, Daya Guo, Duyu Tang, Nan Duan, Xiaocheng Feng, Ming Gong, Linjun Shou, Bing Qin, Ting Liu, Daxin Jiang, Ming Zhou, [Research Center for Social Computing and Information Retrieval, Harbin Institute of Technology, China, The School of Data and Computer Science, Sun Yat-sen University, China, Microsoft Research Asia, Beijing, China, Microsoft Search Technology Center Asia, Beijing, C..
 Longformer: The Long-Document Transformer
Longformer: The Long-Document Transformer
Iz Beltagy, Matthew E. Peters, Arman Cohan [Allen Institute for Artificial Intelligence, Seattle, WA, USA] (2020.04) Abstract Transformer 기반 모델은 sequence 길이에 따라 quadratic 하게 증가하는 계산 복잡도를 가지는 self-attention 연산으로 인해 긴 sequence를 처리하지 못하였다 sequence length에 따라 선형적으로 계산량이 증가하여 수천 개 이상의 토큰을 처리할 수 있는 Longformer를 제시 Longformer의 attention 메커니즘은 drop-in replacement, local windowed attention text8, enwik8에서..
 Few-Shot Font Generation by Learning Fine-Grained Local Styles
Few-Shot Font Generation by Learning Fine-Grained Local Styles
Licheng Tang, Yiyang Cai, Jiaming Liu, Zhibin Hong, Mingming Gong, Minhu Fan, Junyu Han, Jingtuo Liu, Errui Ding, Jingdong Wang [Baidu Inc, University of California, Berkeley, University of Melbourne] (2022.05) Abstract **Few-shot font generation(FFG)**는 노동 cost를 크게 줄여주어 주목을 받고 있는 기술 이전의 연구들은 reference glyph의 content와 style을 global, component-wise하게 disentangle 하는 방식으로 FFG에 접근 하지만 glyph의 style은 ..
