| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- userwidget
- 생성모델
- Font Generation
- RNN
- 딥러닝
- UE5
- WBP
- NLP
- ue5.4
- multimodal
- BERT
- animation retargeting
- dl
- GAN
- Diffusion
- cv
- Generative Model
- ddpm
- 폰트생성
- 언리얼엔진
- 오블완
- motion matching
- CNN
- WinAPI
- Few-shot generation
- 디퓨전모델
- Stat110
- deep learning
- 모션매칭
- Unreal Engine
- Today
- Total
목록전체 글 (220)
Deeper Learning
 [UE5] Enhanced Input(향상된 입력)
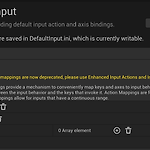
[UE5] Enhanced Input(향상된 입력)
언리얼 엔진 4에서 사용하던 Axis, Action Mapping은 UE5에서 deprecated로대신 Enhanced Input을 사용하는 것을 권장하고 있다. Enhanced Input의 주요 컨셉은 아래와 같다. Input Action: 프로젝트 코드와 Enhanced Input system을 연결해 주는 역할을 하며 캐릭터가 취할 수 있는 점프, 이동, 문 열기 등 Action을 말한다 Input Mapping Contexts: 유저의 입력과 Actions을 매핑하는 역할을 하며 동적으로 추가, 제거가 가능하며 priority 또한 설정이 가능하다. 동일한 키를 입력하였을 때, 문을 열거나, 인벤토리의 아이템을 선택하는 기능을 구현하기 위해서 이전에는 현재의 상태를 정의하는 Boolean 변수를 ..
 References의 주소
References의 주소
간단한 C 공부를 마치고 C++ 문법에 대해 학습중이다. 모든 문법에 대해 포스팅을 하기 보다는 바로 받아들이지 못한, 의문이 생긴 개념에 대해 찾아보고 해결해가는 과정을 포스팅을 남기려한다 Question Reference의 메모리 주소를 디버깅해보니 Initialize한 변수의 주소값과 동일함. References 아래 예시코드 부터 보자 #include void byPointer(int* ptr) { *ptr = 20; } void byReference(int& ref) { ref = 30; } int main() { int num = 10; // 0x0000009EE52FF7D4 / 1E 00 00 00 int* ptr = # byPointer(ptr); std::cout
 Visual Studio 메모리 확인 방법, 32bit 64bit 운영체제
Visual Studio 메모리 확인 방법, 32bit 64bit 운영체제
파이썬 인공지능 개발자, 리서쳐로 쭉 일을 해오다 보니 수학, 통계, 논문에 쓰는 시간이 매우 많아 비교적 타 개발자보다 다른 프로그래밍 언어, CS에 대한 지식이 부족하다고 느껴왔다.3년만에 다시 배우는 C/C++ & 기초 CS에 대한 정리 / 현재 참여중인 언리얼엔진 기반 게임개발 학습 관련해서 포스팅을 블로그에 이어 작성하고자 합니다 Visual Studio 2022 디버그에서 메모리 확인법 F9를 눌러 원하는 line에서 Breakpoint를 걸고 F5를 눌러 디버깅 시작.Breakpoint에 멈춰있는 상태에서 상단 디버그 -> 창 -> 메모리 -> 메모리1,2,3,4 모두 동일 (개발자 편의를 위한 창들) 우측 주소창에 변수명을 입력하거나 변수를 클릭 후 드래그하면 해당 변수의 메모리 주소를 ..
 SVM: Support Vector Machine (1)
SVM: Support Vector Machine (1)
Support Vector Machine 빨간점, 녹색점이 각각 negative, positive class이며 feature의 dimension이 2인 데이터를 나타낸 그림이 있다. 성능이 좋은 분류모델의 Decision boundary를 그린다고 하면 보통 위의 실선을 그리게 될 것인데 이 때, 경계 주변의 점들이 주로 decision boundary의 개형을 결정하게 된다. 이를 모델링 한것이 Support vector machine이다 (이하 SVM) Separate Hyperplane Constraints 위의 예시는 2차원으로 class를 나누는 경계인 hyperplane이 line으로 표현되며, 3차원에서는 plane이 hyperplane이 될 것이다. SVM의 목표는 데이터를 잘 분류할 수..
 직관과 MLE, MAP(2)
직관과 MLE, MAP(2)
(이전글에 이어서 작성) 여기에서 의문이 생기는데 동전을 5번 던져서 모두 앞면이 3번 나오면 MLE 관점으로는 60% 확률로 앞면이 나온다고 추정하고 동전을 100번 던져서 앞면이 60번 나올 때도 마찬가지로 60% 확률로 앞면이 나온다고 추정하는데 괜찮은가 동전은 보통 50% 확률로 앞면이 나온다는 사전지식이 있는데 n 이 작을 때 이 결과를 신뢰해도 괜찮은가 위 의문은 모두 사전지식(prior knowledge)을 반영하지 않기 때문에 생기는 의문으로 사전지식을 반영하여 최적의 추정값을 고르는 다음 글에서는 이어서 MAP 관점으로 다시 문제를 해결해 보겠다. 사전지식을 포함하여 모델링할 때는 Bayes Rule을 사용한다 $$ P(\theta|D) = \frac{P(D|\theta)P(\thet..
동전을 5번 던져서 앞면, 앞면, 뒷면, 앞면, 뒷면이 나왔을 때, 동전을 한 번 던져서 앞면이 나올 확률을 추정하면 직관적으로 3/5라고 생각하는데 정말 그럴까? 위 질문에 대한 답을 MLE 관점으로 찾아보자. Binomal Distribution, Bernoulli experiment 한 번 동전을 던지면 앞면(H) 또는 뒷면(T)가 나오게 되는데, 이는 discrete하고 가능한 값이 2개(H,T)가 전부인 베르누이 분포를 따른다. 매 시행이 동일한 베르누이 분포를 따르며 독립적이기 때문에 동전을 5번 던질 때 1,2,3,4,5 번째 시행에서 동전이 앞면이 나오는 횟수를 나타내는 확률변수 X1,X2,X3,X4,X5 는 i.i.d이기 때문에 동전을 5번 던질 때 앞면이 나오는 횟수를 나타..
 LDM: High-Resolution Image Synthesis with Latent Diffusion Models
LDM: High-Resolution Image Synthesis with Latent Diffusion Models
Robin Rombach, Andreas Blattmann, Dominik Lorenz, Patrick Esser, Björn Ommer, (2021.12) [Ludwig Maximilian University of Munich & IWR, Heidelberg University, Runway ML] (이전 Diffusion Models paper review(DDPM, DDIM, Improved-DDPM 등)에서 다루었던 중복된 내용은 자세하게 적지 않았음) Abstract Diffusion model은 이미지 생성에서 좋은 성능을 보였고 재학습 없이 guidance를 주어 이미지 생성 프로세스를 조정할 수 있는 능력 또한 갖추고 있다 하지만 pixel level에서의 연산이 이루어지기 때문에 수백일의..
 Score-Based Generative Modeling through Stochastic Differential Equations
Score-Based Generative Modeling through Stochastic Differential Equations
Yang Song, Jascha Sohl-Dickstein, Diederik P. Kingma, Abhishek Kumar, Stefano Ermon, Ben Poole, (2020.11) [Stanford, Google] Why score function? 생성모델을 학습한다는 것은 데이터 분포 pθ(x) 를 근사하는 것과 같다. likelihood based 모델에서는 직접적으로 pmf 또는 pdf를 모델링하는데 아래 식처럼 학습가능한 parameter set θ 로 parameterize된 Real-valued function fθ(x) 를 사용하여 pdf를 정의할 수 있다. $$ p_\theta(x) = \frac{e^{-f_\theta}(x)}{Z_\th..
 Score-based Generative Models과 Diffusion Probabilistic Models과의 관계
Score-based Generative Models과 Diffusion Probabilistic Models과의 관계
Generative Modeling by Estimating Gradients of the Data Distribution https://arxiv.org/abs/1907.05600 Score-based Generative Model의 개념을 소개한 논문 Given this dataset, the goal of generative modeling is to fit a model to the data distribution such that we can synthesize new data points at will by sampling from the distribution. 생성모델에서 목표는 주어진 데이터셋을 활용하여 모델이 데이터 분포를 실제 데이터 분포와 가깝게 근사하고 구한 데이터 분포를 활용하여..
 Diffusion Models Beat GANs on Image Synthesis
Diffusion Models Beat GANs on Image Synthesis
Prafulla Dhariwal, Alex Nichol, (2021.05) [OpenAI] Abstract Diffusion 모델이 현재 SOTA 생성 모델을 뛰어넘는 샘플 이미지 퀄리티를 달성할 수 있음을 본 논문에서 소개 unconditional image 생성에서는 Ablation study를 통해 찾은 더 나은 아키텍처를 적용하였고 conditional image 생성에서 classifier의 gradient를 활용하여 더 좋은 샘플 퀄리티와, fidelity & diversity trade-off를 조정할 수 있는 classifier-guidance를 제시 Diffusion 모델의 장점은 distribution coverage를 유지한 채 25 forward step만으로도 BigGAN-deep..
 Improved-DDPM: Improved Denoising Diffusion Probabilistic Models
Improved-DDPM: Improved Denoising Diffusion Probabilistic Models
Alex Nichol, Prafulla Dhariwal (2021.02) [openAI] Abstract DDPM이 간단한 변경으로 높은 log-likelihoods 달성할 수 있다는 것을 보임 reverse diffusion 과정의 분산을 학습하면 더 적은 forward process로 큰 퀄리티 차이 없이 sampling이 가능하다는 것을 발견 GAN과 DDPM이 얼마나 타겟 분포를 커버하는지 비교하기 위해 precision, recall 사용 연산량, model capacity에 따라 샘플 퀄리티와 likelihood가 부드럽게 scaling 되는 것을 확인 https://github.com/openai/improved-diffusion GitHub - openai/improved-diffusion..
 DDIM: Denoising Diffusion Implicit Models
DDIM: Denoising Diffusion Implicit Models
Jiaming Song, Chenlin Meng & Stefano Ermon, (2020.10) [Stanford University] Abstract DDPM(Denoising diffusion probabilistic models)은 adversarial 학습 없이 고품질의 이미지 생성에 성공하였으나 sample을 만들기 위해 많은 스텝의 Markov chain을 거쳐야 하는 문제가 존재 sampling을 빠르게 하기 위해 저자는 DDIM(denoising diffusion implicit models)을 제시 DDPM에서 생성 과정은 Markovian diffusion process의 역으로 정의되어있음 DDIM은 DDPM을 non-Markovian diffusion process의 class로 일..
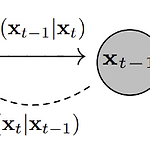 Diffusion Model 수식 정리
Diffusion Model 수식 정리
prerequisite: Diffusion Model에 대한 기초적인 이해 Diffusion Model T = 전체 Timesteps 수 xT = forward process를 T 번 적용한 마지막 Timestep T 에서의 이미지 x0 = 원본 이미지 Forward Process q(xt|xt−1)=N(xt,√1−βtxt−1,βtI) β 는 noise(variance)의 강도를 조절하는 parameter로 DDPM 논문에서는 0.0001 ~ 0.02의 값을 사용 β 가 선형적으로 timesteps에 따라(DDPM에서는 linear noise scheduler 사용) 0.0001에서 0.02까지 증가하..
 [Statistics 110] Lecture 33: Markov Chains Continued Further
[Statistics 110] Lecture 33: Markov Chains Continued Further
Reversible Markov Chains i,j state 간 edge가 없으면 가중치 wij=0. i에서 j state로 wij에 비례하는 확률로 이동. qij=wij∑kwik si는 ∑Kwik에 비례 간단하게 말하면 모든 가역적 마르코프 체인을 아래 형태(가중치가 있는 Random walk)로 나타낼 수 있다. P(Xn+1=j|Xn=i)=wij∑kwik=qij Non-reversible Markov Chains Google PageRank 모든 페이지에 중요도 점수를 주고 그에 따라 검색 결과를 노출. 점수는 참조된 페이지의 수와 그 페이..
 [Statistics 110] Lecture 32: Markov Chains Continued
[Statistics 110] Lecture 32: Markov Chains Continued
Markov Chains States (2),(3)를 보면 특정 state에서 다른 특정 state로는 절대 갈 수 없다. 이러한 상태를 reducible이라고 하고 (1)번과 같이 그렇지 않은 상태를 irreducible이라고 부른다. 어떤 state에서 다시 해당 state로 돌아오는 확률이 1일 때, recurrent state(재귀 상태)라고 부른다. → state 수가 유한하고 irreducible한 마르코프 체인은 모든 state가 recurrent state recurrent state의 반대 개념은 transient state(일시적 상태) (2)번 예시에서 3에서 6으로 가는 루트가 생긴다면 1,2,3은 transient state. (3)번 예시에서 0이나 3에 도달하면 그 상태에 영원..
 [Statistics 110] Lecture 31: Markov Chains
[Statistics 110] Lecture 31: Markov Chains
Markov Chains X0,X1,...에서 Xn을 discrete time n에서의 state라고 생각 Markov Property P(Xn+1=j|Xn=in,Xn−1=in−1,...X0=i0)=P(Xn+1=j|Xn=in)=qij 과거의 모든 정보가 주어졌을 때 다음 state에 대한 확률은 현재 state만 아는 경우에서의 다음 state 확률과 동일 = (과거와 미래는 현재의 상태가 주어졌을 때 조건부 독립이 성립) qij는 Transition probability(전이확률)로 시간과 독립(n에 독립)으로 이러한 마르코프 체인을 동질 마르코프 체인이라고 부름 그림을 보면 직관적으로 이해가 되는데, state 1, 2, ..
 [Statistics 110] Lecture 30: Chi-Square, Student-t, Multivariate Normal
[Statistics 110] Lecture 30: Chi-Square, Student-t, Multivariate Normal
Chi-Square Distribution(카이제곱 분포) V=Z21+...+Z2n, Zj∼N(0,1)i.i.d일 때, V∼χ2(n). χ2(1)은 Gamma(12,12)와 같은 분포, χ2는 Gamma(n2,12)와 같은 분포 t-Distribution(t-분포) Z∼N(0,1)V∼χ2(n)T=Z√V/n∼tn 성질 Symmetric: −T∼tn. n=1이면 코시분포를 따름 n이 2이상이면 E(T)=0. 정규분포와 비슷하지만 더 heavy tailed(극단..
 [Statistics 110] Lecture 29: Law of Large Numbers and Central Limit Theorem
[Statistics 110] Lecture 29: Law of Large Numbers and Central Limit Theorem
Law of Large Numbers(큰 수의 법칙) X1,...,Xn이 i.i.d 이며 평균 μ, 표준편차 σ2일 때, 표본평균 ˉXn=1n∑nj=1Xj라고 정의 Strong LLN: n이 무한으로 가면 1의 확률로 ˉXN 이 μ로 간다. (표본평균이 모평균에 근사) Weak LLN: 모든 c>0에 대해 n이 무한으로 가면, P(|ˉXn−μ|>c)→0. 체비셰프 부등식을 활용한 Weak LLN 증명 ˉXn−μ가 0으로 수렴한다는 것은 알지만, ˉXn 분포에 대한 정보는 아직 알 수 없음 무한으로 가는 무언가와 곱하여 힌트를 얻을 수 있음 ..
 [Statistics 110] Lecture 28: Inequalities
[Statistics 110] Lecture 28: Inequalities
Conditional Expected value 특정 기간동안 방문한 손님의 수를 N, Xj를 j번째 고객이 소비하는 비용이라고 하자(평균은 μ, 분산은 σ2) N,X1,...,Xn은 서로 독립일 때 X=∑Nj=1Xj의 평균과 분산을 구하여라. E(X)= Adam’s Law를 활용해도 같은 결과를 얻을 수 있다. E(X) = E(E(X|N)) = E(\mu N) = \mu E(N) EVE’s Law로 분산을 구해보자 $$ Var(X) = E(Var(X|N)) + Var(E(X|N)) \\ = E(N \sigma^2) + Var(\mu N) = \si..
 [Statistics 110] Lecture 27: Conditional Expectation given an R.V.
[Statistics 110] Lecture 27: Conditional Expectation given an R.V.
Conditional Expectation X \sim N(0,1), Y=X^2이면 E(Y|X) = E(X^2|X) = X^2 = Y \\E(X|Y) = E(X|X^2) = 0. 바로 위 식이 0이되는 이유는 X^2이 a라고 생각해보면 X = \pm \sqrt a이며 따라서 X의 기댓값은 둘의 평균인 0이 된다. 막대 부러뜨리기 문제 길이가 1인 막대를 무작위 지점에서(Uniform) 부러뜨린다. 부러뜨려 얻은 좌측 조각을 다시 무작위 지점에서 부러뜨려 얻은 막대 조각의 길이의 기댓값은? 첫 번째로 부러뜨리는 지점을 X, 두 번째로 부러뜨리는 지점을 Y라고 하자. $$ X \sim Unif(0,1)\\Y|X \sim Unif(0,X)\\E(Y|X=x) = \frac x2\\E..
 [Statistics 110] Lecture 25: Order Statistics and Conditional Expectations
[Statistics 110] Lecture 25: Order Statistics and Conditional Expectations
Beta Distribution & Gamma Distribution 베타분포와 감마분포의 관계 Bank-post office example 은행 대기시간을 X \sim Gamma(a, \lambda), 우체국 대기시간을 Y \sim Gamma(b,\lambda). X,Y는 독립일 때, T = X+Y, W = \frac{X}{X+Y}의 joint distribution을 구하여라 계산의 편의를 위해 \lambda를 1로 두고 시작한다. f_{T,W}(t,w) = f_{X,Y}(x,y)|\frac{d(x,y)}{d(t,w)}| = \frac{1}{\Gamma(a)\Gamma(b)}x^ae^{-x}y^be^{-y}\frac1{xy}|J| Jacobian을 구하고 식을 이어서 풀면..
2 Envelope Paradox X,Y 두 봉투가 있고 하나의 봉투에는 다른 봉투의 2배의 돈이 들어있다. 모순 E(Y) = E(X)\\E(Y) = E(Y|Y=2X)P(Y=2X)+E(Y|Y= \frac X2)P(Y= \frac X2) = \frac 12E(2X)+ \frac 12 E(\frac X2) = \frac 54 E(X) 대칭성에 의해 첫 번째식이 맞고 두 번째 식은 LOTP에 의해 맞는 것 같지만 두 번째식은 틀린 식 E(Y|Y=2X) \ne E(2X). 서로 독립이라는 근거가 없기 때문에 불가능. Patterns in Coin Flips 특정 패턴이 나오기 까지(HT) 얼마나 동전을 많이 던졌을까? W_{HT}를 HT 패턴이 나오기까지 동전을 던진 횟수를 나타내는 확률변..
 DDPM: Denoising Diffusion Probabilistic Models
DDPM: Denoising Diffusion Probabilistic Models
Jonathan Ho, Ajay Jain, Pieter Abbeel, (2020.06) [UC Berkeley] [이후 Cold Diffusion 논문에서 Gaussian Noise가 아닌 다른 Noise를 사용하여 학습이 가능함을 보였기 때문에, 해당 파트에 대한 수식은 간단하게 다룸, Langevin dynamics 또한 다루지 않음] Abstract 비평형 열역학에서 영감을 받은 latent variable model인 diffusion 확률 모델을 사용한 고품질의 이미지 생성 방법론을 제시 diffusion 확률 모델, denoising score matching, Langevin dynamics의 관계를 활용하여 디자인한 weighted variational bound로 학습 CIFAR-10 u..
Gamma Function(감마 함수) \Gamma (a) = \int_0^{\inf}x^ae^{-x}\frac{dx}{x}, (a>0,\R) 성질 \Gamma(n) = (n-1)!\\ \Gamma(x+1) = x\Gamma(x)\\ \Gamma(1/2) =\sqrt \pi Gamma Distribution(감마 분포) 모든 가능한 구간에 대해 적분값이 1이 되도록 정규화 하기 위해 간단하게 감마 함수를 감마함수로 나누면 \int_0^{\inf}\frac1{\Gamma(a)}x^ae^{-x}\frac{dx}{x} = 1\\p.d.f\space f_X(x) = \frac1{\Gamma(a)}x^ae^{-x}\frac{1}{x} X \sim Gamma(a,1)의 pdf식을..
 [Statistics 110] Lecture 23: Beta distribution
[Statistics 110] Lecture 23: Beta distribution
Beta Distribution(베타분포) Uniform distribution의 일반화 버전 Beta(a,b), a>0, b>0. PDF $f(x) = cx^{a-1}(1-x)^{b-1}, 0
 [Statistics 110] Lecture 22: Transformations and Convolutions
[Statistics 110] Lecture 22: Transformations and Convolutions
초기하분포 분산 저번 강의에 이어서 식 정리 $$ Var(X) = Var(X_1+...+X_n) = Var(X_1)+...+Var(X_n)+2\sum_{i0임을 보이면 된다. 각 물체에 “점수”가 있다고 가정한다. 좋은 점수(평균 이상)의 점수를 가지는 object는 무조건 1개 이상 존재한다. 예시) 100명의 사람들, 15개의 위원회가 있고 한 사람이 3개에 위원회에 속해있다면 겹치는 사람이 3명보다 많은 위원회가 존재한다는것을 보여라 임의의 두 위원회에서 겹치는 사람의 기댓값을 구하자. 사람 j가 특정 위원회 2개에 동시에 속해있는 사건을 나타내는 지시확률변수 X_j를 설정 $ X_j = \frac{\binom32}{\binom{100}2} \\ E(X) = E(X_1)+...+E(X_{10..
Covariance(공분산) 정의 Cov(X,Y) = E((X-E(X))(Y-E(Y))) = E(XY) - E(X)E(Y) 성질 $$ Cov(X,X) = Var(X)\\Cov(X,Y) = Cov(Y,X)\\Cov(X,c) = 0,(c=constant)\\Cov(cX,Y) = cConv(X,Y)\\Cov(X,Y+Z) = Cov(X+Y)+Cov(X,Z)\\Cov(X+Y,Z+W) = Cov(X,Z)+Cov(X,W)+Cov(Y,Z)+Cov(Y,W)\\Cov(\sum_{i=1}^ma_iX_i, \sum_{j=1}^nb_jY_j) = \sum_{i,j}a_ib_jCov(X_i,Y_j)\\Var(X_1+X_2) = Cov(X_1+X_2,X_1+X_2) = Cov(X_1,X_1)+2Cov(X_1,X_2)+C..
2-D LOTUS Z_1,Z_2가 i.i.d 표준정규분포를 따를 때, E(|Z_1-Z_2|)를 구하라 X,Y가 서로 독립이고 정규분포를 따를 때, X+Y \sim N(\mu_1+\mu_2,\sigma_1^2+\sigma_2^2). Z_1-Z_2는 N(0,2)를 따르기 때문에 Z = \frac{x-\mu}{\sigma}에서 N(0,2)=\sqrt2Z. \sqrt2 E(|Z|) = \sqrt2\int_{-\inf}^{inf}|z|\frac{1}{\sqrt{2\pi}}e^{-z^2/2}dz\\=\sqrt{\frac2\pi} Multinomial Distribution(다항분포) $\vec X\sim Mult(n,\vec p), \vec p=(p_1,...,p_k), p_j ..
 [Statistics 110] Lecture 19: Joint, Conditional, and Marginal Distributions
[Statistics 110] Lecture 19: Joint, Conditional, and Marginal Distributions
Joint, Conditional, Marginal Distribution joint CDF(discrete & continuous) F(x,y) = P(X \le x, Y \le y) joint PDF(continuous) f(x,y) = \frac{d}{dxdy}F(x,y)\\P((x,y) \in A) = \int\int_Af(x,y)dxdy marginal PDF of X \int f(x,y)dy PDF of conditional distribution Y|X 독립 f(x,y)= \frac1\pi,(x^2+y^2\le1, 0 \space otherwise). 위 식에서 X의 marginal distribution을 구하면 $$ f_X(x) = \int_{-\sqr..
